题目内容
【题目】已知⊙O的半径为2,∠AOB=120°.
(1)点O到弦AB的距离为______ ;
(2)若点P为优弧AB上一动点(点P不与A、B重合),设∠ABP=α,将△ABP沿BP折叠,得到A点的对称点为A′;
①若∠α=30°,试判断点A′与⊙O的位置关系;
②若BA′与⊙ O相切于B点,判断△ABP的形状;

【答案】(1)1;(2)①点A′在⊙O上;②△PAB为等边三角形
【解析】试题分析:(1)如图,作辅助线;证明∠AOC=60°,得到OC=1;
(2)①证明∠PAB=90°,得到PB是⊙O的直径;证明∠PA′B=90°,即可解决问题.
②证明∠A′BP=∠ABP=60°;借助∠APB=60°,即可得到△PAB为正三角形.
试题解析:(1)如图,过点O作OC⊥AB于点C;
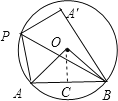
∵OA=OB,
则∠AOC=∠BOC=![]() ×120°=60°,
×120°=60°,
∵OA=2,
∴OC=1.
故答案为1.
(2)①∵∠AOB=120°,
∴∠APB=![]() ∠AOB=60°,
∠AOB=60°,
∵∠PBA=30°,
∴∠PAB=90°,
∴PB是⊙O的直径,
由翻折可知:∠PA′B=90°,
∴点A′在⊙O上.
②由翻折可知∠A′BP=∠ABP,
∵BA′与⊙O相切,
∴∠OBA′=90°,
∴∠ABA′=120°,
∴∠A′BP=∠ABP=60°;
∵∠APB=60°,
∴△PAB为等边三角形.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

