题目内容
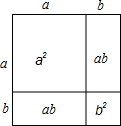利用右图可以证明等式：a2+2ab+b2=（a+b）2．（1）图中大正方形的面积既可以表示为：
a2+2ab+b2
a2+2ab+b2
，又可以表示为：（a+b）2
（a+b）2
，从而证明a2+2ab+b2=（a+b）2；
（2）请画出一个图形来计算：（a+b+c）2．（在图上标注必要的字母）
分析：（1）图中大正方形的面积可以用正方形的面积公式来求，也可把正方形分成四个小图形分别求出面积再相加，从而得出（a+b）2=a2+2ab+b2；
（2）直接作图即可得出（a+b+c）2=a2+b2+c2+2ab+2bc+2ac成立．
（2）直接作图即可得出（a+b+c）2=a2+b2+c2+2ab+2bc+2ac成立．
解答：解：（1）边长为（a+b）的正方形的面积可以直接由正方形面积公式表示为（a+b）2；
又可以用边长为a的正方形的面积，减去2个长为a，宽为b的长方形面积，加上边长为b的正方形的面积，
结果用含a，b的式子表示为a2+2ab+b2；
故答案为a2+2ab+b2、（a+b）2
（2）已知大正方形的边长为a+b+c，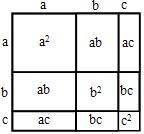
利用图形的面积关系可得：（a+b+c）2=a2+b2+c2+2ab+2bc+2ac．
又可以用边长为a的正方形的面积，减去2个长为a，宽为b的长方形面积，加上边长为b的正方形的面积，
结果用含a，b的式子表示为a2+2ab+b2；
故答案为a2+2ab+b2、（a+b）2
（2）已知大正方形的边长为a+b+c，
利用图形的面积关系可得：（a+b+c）2=a2+b2+c2+2ab+2bc+2ac．
点评：本题考查了完全平方公式的几何意义，是对（a-b）2=a2-2ab+b2和（a+b+c）2=a2+b2+c2+2ab+2bc+2ac的几何证明．
练习册系列答案
相关题目
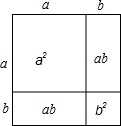利用右图可以证明等式：a2+2ab+b2=（a+b）2．