题目内容
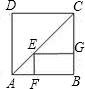
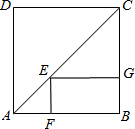
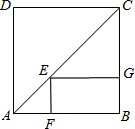 如图,正方形的周长为8cm,则矩形EFBG的周长为________.
如图,正方形的周长为8cm,则矩形EFBG的周长为________.
4cm
分析:由正方形的性质可以得出∠ACB=∠BAC=45°,AB=BC=2,由矩形的性质可以得出,∠EFB=∠EGB=90°,EG=FB,FE=GB,可以得出△AEF与△GEC是等腰直角三角形,可以得出EF=AF,EG=CG,从而可以得出结论.
解答:∵四边形ABCD是正方形,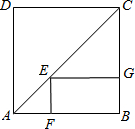
∴AB=BC=CD=AD,∠B=90°,∠ACB=∠BAC=45°.
∵正方形ABCD的周长为8cm,
∴AB=BC=CD=AD=2cm.
∵四边形EFBG是矩形,
∴EG=FB,FE=GB,EG∥FB,FE∥GB,
∴∠AFE=∠EGC=90°,
∴∠AEF=∠GEC=45°,
∴∠FAE=∠FEA,∠GEC=∠GCE,
∴AF=EF,GE=GC.
∵C矩形EFBG=EG+FE+FB+GB,
∴C矩形EFBG=AF+FB+GB+GC=AB+BC=2+2=4cm.
故答案为:4cm.
点评:本题考查了正方形的性质的运用及正方形的周长的运用,矩形的性质的运用,等腰三角形的性质的运用,解答时合理运用等腰三角形的性质是解答本题的关键.
分析:由正方形的性质可以得出∠ACB=∠BAC=45°,AB=BC=2,由矩形的性质可以得出,∠EFB=∠EGB=90°,EG=FB,FE=GB,可以得出△AEF与△GEC是等腰直角三角形,可以得出EF=AF,EG=CG,从而可以得出结论.
解答:∵四边形ABCD是正方形,

∴AB=BC=CD=AD,∠B=90°,∠ACB=∠BAC=45°.
∵正方形ABCD的周长为8cm,
∴AB=BC=CD=AD=2cm.
∵四边形EFBG是矩形,
∴EG=FB,FE=GB,EG∥FB,FE∥GB,
∴∠AFE=∠EGC=90°,
∴∠AEF=∠GEC=45°,
∴∠FAE=∠FEA,∠GEC=∠GCE,
∴AF=EF,GE=GC.
∵C矩形EFBG=EG+FE+FB+GB,
∴C矩形EFBG=AF+FB+GB+GC=AB+BC=2+2=4cm.
故答案为:4cm.
点评:本题考查了正方形的性质的运用及正方形的周长的运用,矩形的性质的运用,等腰三角形的性质的运用,解答时合理运用等腰三角形的性质是解答本题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目

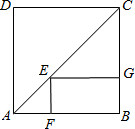 如图,正方形的周长为8cm,则矩形EFBG的周长为
如图,正方形的周长为8cm,则矩形EFBG的周长为