题目内容
(2013•内江)某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
| X | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
分析:(1)设y与x之间的函数关系式为y=kx+b,运用待定系数法就可以求出y与x之间的函数关系式;
(2)设原计划要m天完成,则增加2km后用了(m+15)天,根据每天修建的工作量不变建立方程求出其解,就可以求出计划的时间,然后代入(1)的解析式就可以求出结论.
(2)设原计划要m天完成,则增加2km后用了(m+15)天,根据每天修建的工作量不变建立方程求出其解,就可以求出计划的时间,然后代入(1)的解析式就可以求出结论.
解答:解:(1)设y与x之间的函数关系式为y=kx+b,由题意,得
,
解得:
,
∴y与x之间的函数关系式为:y=-
x+50(30≤x≤120);
(2)设原计划要m天完成,则增加2km后用了(m+15)天,由题意,得
=
,
解得:m=45
经检验m=45是原方程的根.
∴原计划每天的修建费为:-
×45+50=41(万元).
|
解得:
|
∴y与x之间的函数关系式为:y=-
| 1 |
| 5 |
(2)设原计划要m天完成,则增加2km后用了(m+15)天,由题意,得
| 6 |
| m |
| 6+2 |
| m+15 |
解得:m=45
经检验m=45是原方程的根.
∴原计划每天的修建费为:-
| 1 |
| 5 |
点评:本题考查了运用待定系数法求函数的解析式的运用,列分式方程解实际问题的运用,设间接未知数在解答运用题的运用,解答时建立分式方程求出计划修建的时间是关键.

练习册系列答案
相关题目
 (2013•内江)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:
(2013•内江)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1: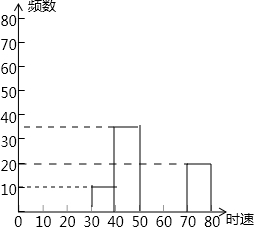 (2013•内江)随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
(2013•内江)随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):