题目内容
若函数y=x2-2x-3的函数值为0,则( )
分析:由已知函数的函数值为0,故令y=0,得到关于x的一元二次方程,求出方程的解即可得到x的值.
解答:解:对于函数y=x2-2x-3,
令y=0,得到x2-2x-3=0,
因式分解得:(x-3)(x+1)=0,
解得:x=3或x=-1.
故选D
令y=0,得到x2-2x-3=0,
因式分解得:(x-3)(x+1)=0,
解得:x=3或x=-1.
故选D
点评:此题考查了抛物线与x轴的交点,要求抛物线与x轴交点的横坐标,即要令二次函数解析式中y=0,得到关于x的一元二次方程,求出方程的解可得.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
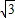 x+1图象与直线
x+1图象与直线 有两个交点,则b为 .
有两个交点,则b为 .