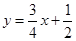题目内容
小虎一家利用元旦三天驾车到某景点旅游,小汽车出发前油箱有油36L,匀速行驶若干小时后,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题:
(1)求油箱余油量Q与行驶时间t之间的函数关系式;
(2)如果出发地距景点200km,车速为80km/h,要到达景点,油箱中的油是否够用?请说明理由.
(1)Q=-10t+36;(2)够用
解析试题分析:(1)设加油前一次函数关系式为Q=kt+b(k≠0),由图可得当t=0时,Q=36,当t=3时,Q=6,根据待定系数求解即可;
(2)先根据图象特征求得到达景点所需时间,再把求得的时间代入(1)中的函数关系式求解即可.
(1)设加油前一次函数关系式为Q=kt+b(k≠0)
∵当t=0时,Q=36,当t=3时,Q=6
∴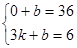 ,解得
,解得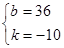
∴一次函数关系式为Q=-10t+36;
(2)∵到达景点需t=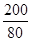 =2.5(h)
=2.5(h)
∴把t=2.5代入Q=-10t+36 中得 Q=11>0
∴要到达景点,油箱中的油够用.
考点:一次函数的应用
点评:一次函数的应用是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
若直线y=3x+m经过第一、三、四象限,则点A(m,1)必在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知k1<0<k2,则函数y=k1x和 的图象大致是( )
的图象大致是( )
A. | B. | C. | D. |
如图,过点Q(0,3.5)的一次函数与正比例函数y=2x的图象相交于点P,能表示这个一次函数图象的解析式是( )
A.y= | B.y= | C.y= | D.y=﹣ |
已知二次函数 的图像如图所示,则一次函数
的图像如图所示,则一次函数 的大致图像可能是
的大致图像可能是
A. | B. | C. | D. |
 的解是 .
的解是 . 万元且不少于
万元且不少于 万元的资金购进这两种彩电共20台,问有哪几种进货方案?
万元的资金购进这两种彩电共20台,问有哪几种进货方案?