��Ŀ����
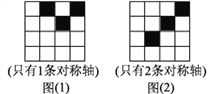
����Ŀ����1����ͼ������4��4�������������У�����2��С�����α�Ϳ��������ֱ�������2��ͼ���ٽ����ɸ��հ�С������Ϳ�ڣ�ʹ��Ϳ�ڵ�ͼ�γ�Ϊ��Գ�ͼ������ͼ��1��Ҫ��ֻ��1���Գ��ᣬͼ��2��Ҫ��ֻ��2���Գ�������

��ֻ��1���Գ��ᣩ ��ֻ��2���Գ��ᣩ
ͼ�� ͼ��
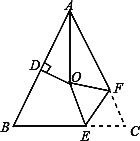
����ͼ��A��BΪֱ��MN�����㣬�ҵ�MN�ľ��벻��ȣ��ֱ���MN����һ��P����������������������ͼ������һ��Pʹ��PA+PB��С�� ����ͼ������һ��Pʹ����PA��PB�������
����д������������ͼ�ۼ���
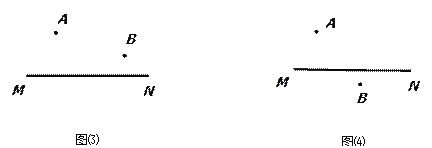
���𰸡�������
�����������������
(1) ����ͼ(1)����ѡ��һ��ֱ����Ϊ����ͼ�εĶԳ������ٽ�����ͼ�ΰ���ѡ��ĶԳ�������Գ���������ͼ��ֻ��һ���Գ��ᣬ��ɰ���ͼ����Ϳ�հ���������ͼ�δ��ڲ�ֻһ���Գ��ᣬ������ѡ��Գ��᳢��. ����ͼ(2)�������ȷ���ԭ��ͼ�εĶԳ��ᣬ����ԭ��ͼ�εĶԳ���Ϊ���գ��۲췽�����ӵ�λ���Ƿ�����ԭͼ�ζԳ��������ı仯���Ӷ�ȷ��ͼ����״.
(2) ����ͼ(3)����һ������Ŀ��������������ԳƵ����ʺ����������߹�ϵ�еġ�����֮�ʹ��ڵ����ߡ��õ���. ������������B����ֱ��MN�ĶԳƵ�B'��Ȼ�������ӵ�B'���A�������߶�AB'��ֱ��MN�Ľ��㼴Ϊ�����P. ����ͼ(4)����һ������Ŀ��������������ԳƵ����ʺ����������߹�ϵ�еġ�����֮��С�ڵ����ߡ��õ���. ������������B����ֱ��MN�ĶԳƵ�B'��Ȼ�����ӵ�B'���A�����ӳ������߶�AB'����ֱ��MN�ཻ���˽��㼴Ϊ�����P.
���������
(1) ��ͼ��ʾ��
(2) ��ͼ��ʾ����P��Ϊ������
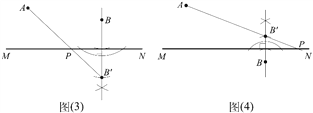
(ע��ͼ�и�����һ�ֳ߹���ͼ�Ľⷨ. ����Ŀ������ȷҪ���ǰ������Ҳ����ʹ�����ǰ�ȹ��߽�����ص���Գ���ͼ.)