题目内容
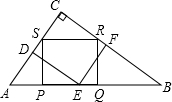
一块直角三角形木块的面积为1.5m2,直角边AB长1.5m,想要把它加工成一个面积尽可能大的正方形桌面,甲、乙两人的加工方法分别如图①、图②所示.你能用所学知识说明谁的加工方法更符合要求吗?
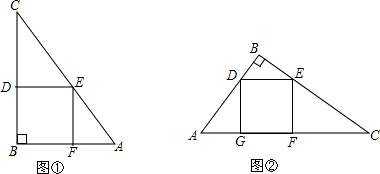
 解:∵直角边AB长为1.5米,面积为1.5平方米,S△ABC=
解:∵直角边AB长为1.5米,面积为1.5平方米,S△ABC= AB•BC,
AB•BC,即
 ×1.5•BC=1.5,
×1.5•BC=1.5,∴BC=2m,AC=
 m,
m,在甲的方法(图①)中,设正方形的边长为y,
∵DE∥AB,
∴
 =
= 即:
即: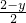 =
=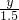 ,
,解得y=
 m,
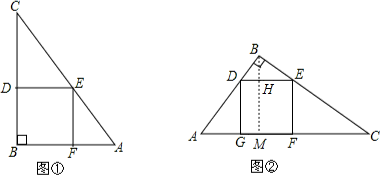
m,在乙的方法(图②)中,设正方形的边长为x,
∴直角△ABC中,AC边上的高BM=
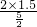 =1.2m.
=1.2m.∵四边形DEFG是正方形,
∴DE∥AC,
∴△BDE∽△BAC,
∴
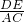 =
=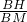 =
=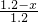 ,
,即
 =
=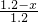 ,
,解得:x=
 .
.∵图①中正方形的边长是
 ,图②中的正方形边长是
,图②中的正方形边长是 ,因为
,因为 >
> ,
,∴甲的加工更符合要求.
分析:由于有正方形的一边平行于三角形的一边,故可用相似三角形的性质求解.
点评:本题考查了相似三角形的应用,解题的关键是利用正方形的性质得到平行线,并进一步得到相似三角形,利用相似三角形的性质进行解题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目