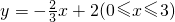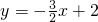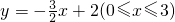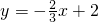题目内容
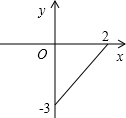 已知变量y与x的函数图象如图所示,则函数关系式为( )
已知变量y与x的函数图象如图所示,则函数关系式为( )| A、y=-3x-3(0≤x≤2) | ||
| B、y=-3x+3 | ||
C、y=
| ||
| D、y=3x+3 |
分析:根据图象可知y是x的一次函数,设函数解析式为y=kx+b,把(2,0),(0,-3)代入y=kx+b,运用待定系数法即可求出函数的解析式,然后根据图象确定x的取值范围.
解答:解:设y=kx+b.
∵图象经过点(2,0),(0,-3),
∴
,
解得
,
∴y=
x-3(0≤x≤2).
故选C.
∵图象经过点(2,0),(0,-3),
∴
|
解得
|
∴y=
| 3 |
| 2 |
故选C.
点评:主要考查了用待定系数法求一次函数的解析式.先设y=kx+b,再结合图象把已知点的坐标代入可求出k,b的值,即得一次函数的解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
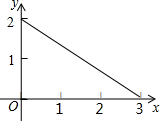 已知变量y与x之间的函数关系的图象如图,它的解析式是( )
已知变量y与x之间的函数关系的图象如图,它的解析式是( )A、y=-
| ||
B、y=-
| ||
C、y=-
| ||
D、y=-
|
 已知变量y与x的函数图象如图所示,则函数关系式为
已知变量y与x的函数图象如图所示,则函数关系式为 x-3(0≤x≤2)
x-3(0≤x≤2) 已知变量y与x之间的函数关系的图象如图,它的解析式是
已知变量y与x之间的函数关系的图象如图,它的解析式是