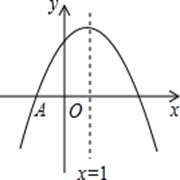题目内容
如图,在平面直角坐标系xOy中,已知抛物线(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x 轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x 轴交于另一点A3;将C3绕点A2旋转180°得C4,与x 轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,Cn,….则点A4的坐标为 ;Cn的顶点坐标为 (n为正整数,用含n的代数式表示) .
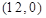 ;
;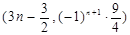 (n为正整数).
(n为正整数).
解析试题分析:令y=0,则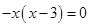 ,解得x1=0,x2=3,
,解得x1=0,x2=3,
∴A1(3,0).
∴根据旋转的性质可得点A4的坐标为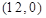 .
.
∵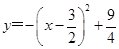 ,∴C1的顶点坐标为
,∴C1的顶点坐标为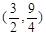 .
.
∴根据旋转的性质可得C2的顶点坐标为 ;C3的顶点坐标为
;C3的顶点坐标为 ;C4的顶点坐标为
;C4的顶点坐标为 ;………Cn的顶点坐标为
;………Cn的顶点坐标为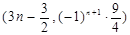 (n为正整数).
(n为正整数).
考点:1.探索规律题(图形的变化类);2.二次函数图象与几何变换.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
抛物线y = - (x+1)2+3的顶点坐标( )
(x+1)2+3的顶点坐标( )
| A.(1,3) | B.(1,-3) | C.(-1,3) | D.(-1,-3) |
 向右平移2个单位,再向上平移2个单位所得抛物线的表达式是 .
向右平移2个单位,再向上平移2个单位所得抛物线的表达式是 .
 分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .
分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .

 可以由抛物线
可以由抛物线 向__________________(平移)得到.
向__________________(平移)得到.
 B.
B.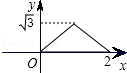 C.
C. D.
D.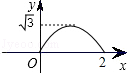
 1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:
1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论: ;④3≤n≤4中,
;④3≤n≤4中,