题目内容
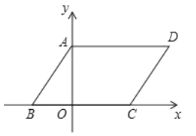
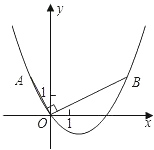
【题目】如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上是否存在点P,使得S△ABP=S△ABO.若存在,请直接写出点P的坐标
【答案】(1)B(4,2);(2)![]() ;(3)P 1 (0,0),P 2 (3,0),
;(3)P 1 (0,0),P 2 (3,0),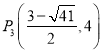 ,
,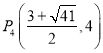
【解析】
(1) 过点A作AF⊥x轴,垂足为点F,过点B作BE⊥x 轴,垂足为点E,则AF=2,OF=1,再证明Rt△AFO∽Rt△OEB,根据相似三角形的性质求得BE=2,OE=4,即可得点B的坐标为(4,2);(2)利用待定系数法求得抛物线的解析式即可;(3)根据三角形的面积公式求得点P的纵坐标只能是0或4,再解方程即可求得点P的坐标.
(1)如图,过点A作AF⊥x轴,垂足为点F,过点B作BE⊥x 轴,垂足为点E,则AF=2,OF=1,
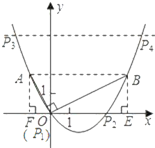
∵OA⊥OB,
∴∠AOF+∠BOE=90°,
又∵∠BOE+∠OBE=90°,
∴∠AOF=∠OBE,
∴Rt△AFO∽Rt△OEB,
∵OB=2OA,
∴![]() ,
,
∴BE=2,OE=4,
∴B(4,2);
(2)设过点A(-1,2),B(4,2),0(0,0)的抛物线为y=ax2 +bx,
∴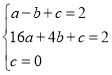 ,
,
解得,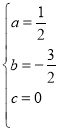 ,
,
∴所求抛物线的表达式为![]() ;
;
(3)∵A (-1,2),B(4,2),
∴AB∥x轴,
设抛物线上符合条件的点P到AB的距离为d,
则S△ABP =![]() ,∴d=2,
,∴d=2,
∴点P的纵坐标只能是0或4,
令y=0,得![]() ,解之,得x=0,或x=3,
,解之,得x=0,或x=3,
∴符合条件的点P1 (0,0),P 2 (3,0),
令y=4,得![]() ,解之,得
,解之,得![]() ,
,
∴符合条件的点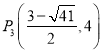 ,
,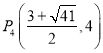 ,
,
∴综上,符合题意的点有四个:P 1 (0,0),P 2 (3,0),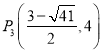 ,
,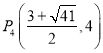 .
.


练习册系列答案
相关题目