题目内容
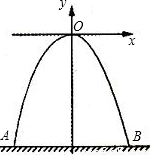
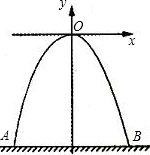 如图所示,有一城门洞呈抛物线形,拱高为4m(最高点到地面的距离),把它放在直角坐标系中,其解析式为y=-x2.
如图所示,有一城门洞呈抛物线形,拱高为4m(最高点到地面的距离),把它放在直角坐标系中,其解析式为y=-x2.
(1)求城门洞最宽处AB的长;
(2)现在有一高2.6m,宽2.2m的小型运货车,问它能否完全通过此城门?请说明理由.
 解:(1)令抛物线y=-x2=-4,
解:(1)令抛物线y=-x2=-4,解得x=±2,
故城门洞最宽处AB的长为4m;
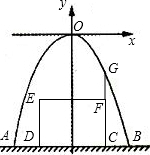
(2)如图,设小货车行驶到城门正中间,用矩形CDEF表示小货车的横截面,
则ED、FC均垂直AB,E、F到AB的距离均为2.6m,F点的横坐标为1.1,
设CF的延长线交抛物线于点G,则点G横坐标为1.1,
∴G点纵坐标为-1.21点G到AB的距离为4-1.21=2.79>2.6,
故小货车能完全通过此城门洞.
分析:(1)令抛物线y=-x2=-4,解得A、B横坐标,可求出城门洞最宽处AB的长,
(2)设小货车行驶到城门正中央,用矩形CDEF表示小货车的横侧面,F点横坐标为1.1,在抛物线上当x=1.1时,求出G点纵坐标和小货车的高CF作比较,得出结论.
点评:本题主要考查二次函数的应用,应用函数问题解决实际问题,比较简单.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
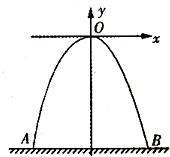 19、如图所示,有一城门洞呈抛物线形,拱高为4m(最高点到地面的距离),把它放在直角坐标系中,其解析式为y=-x2.
19、如图所示,有一城门洞呈抛物线形,拱高为4m(最高点到地面的距离),把它放在直角坐标系中,其解析式为y=-x2.