题目内容
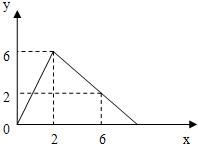 23、某医院研究所开发了一种新药,在实验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)的变化情况如图所示.
23、某医院研究所开发了一种新药,在实验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)的变化情况如图所示.(1)服药后
2
小时,血液中含药量最高,接着逐步衰减;(2)服药后6小时,血液中含药量达到每毫升
2
微克;(3)当0≤x≤2时,y与x之间的函数关系式是
y=3x
;(4)当x≥2时,y与x之间的函数关系式是
y=-x+8
;(5)如果每毫升血液中的含药量3微克或3微克以上时,治疗疾病最有效,那么这个最有效的时间共有
4
小时.分析:(1)看函数图象最高点所对应的自变量的取值即可;
(2)找到自变量x=6时,所对应的函数图象上的函数值即可;
(3)设出正比例函数解析式,把(2,6)代入即可求解;
(4)设出一次函数解析式,把(2,6)(6,2)代入即可求解;
(5)把y=3代入所得的两个函数解析式,看得到的相应时间,较大的数减较小的数即为有效时间.
(2)找到自变量x=6时,所对应的函数图象上的函数值即可;
(3)设出正比例函数解析式,把(2,6)代入即可求解;
(4)设出一次函数解析式,把(2,6)(6,2)代入即可求解;
(5)把y=3代入所得的两个函数解析式,看得到的相应时间,较大的数减较小的数即为有效时间.
解答:解:(1)由图象可以看出:服药后2小时,血液中含药量最高,接着逐步衰减;
(2)由图象可以看出:服药后6小时,血液中含药量达到每毫升2微克;
(3)设正比例函数解析式为y=kx,把(2,6)代入得,k=3,
∴当0≤x≤2时,y与x之间的函数关系式是y=3x;
(4)设一次函数解析式为y=kx+b,
∵(2,6)(6,2)在函数解析式上,
∴2k+b=6,6k+b=2,
解得k=-1,b=8,
∴当x≥2时,y与x之间的函数关系式是y=-x+8;
(5)把y=3代入y=3x得,x=1;
把y=3代入y=-x+8得x=5,
∴有效时间为5-1=4,
∴如果每毫升血液中的含药量3微克或3微克以上时,治疗疾病最有效,那么这个最有效的时间共有4小时.
(2)由图象可以看出:服药后6小时,血液中含药量达到每毫升2微克;
(3)设正比例函数解析式为y=kx,把(2,6)代入得,k=3,
∴当0≤x≤2时,y与x之间的函数关系式是y=3x;
(4)设一次函数解析式为y=kx+b,
∵(2,6)(6,2)在函数解析式上,
∴2k+b=6,6k+b=2,
解得k=-1,b=8,
∴当x≥2时,y与x之间的函数关系式是y=-x+8;
(5)把y=3代入y=3x得,x=1;
把y=3代入y=-x+8得x=5,
∴有效时间为5-1=4,
∴如果每毫升血液中的含药量3微克或3微克以上时,治疗疾病最有效,那么这个最有效的时间共有4小时.
点评:用到的知识点为:过原点的直线解析式的一般形式为y=kx(k≠0);直线解析式的一般形式为y=kx+b(k≠0);点在函数解析式上,点的横纵坐标就适合这个函数解析式.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
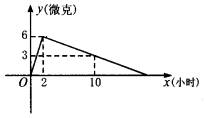
 血液中含药量y(微克)随时间x(小时)的变化情况如图所示.
血液中含药量y(微克)随时间x(小时)的变化情况如图所示.