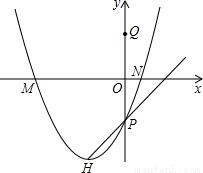
题目内容
已知⊙T与坐标轴有四个不同的交点M、P、N、Q,其中P是直线y=kx-1与y轴的交点, 点Q与点P关于原点对称.抛物线y=ax2+bx+c经过点M、P、N,其顶点为H.
点Q与点P关于原点对称.抛物线y=ax2+bx+c经过点M、P、N,其顶点为H.(1)求Q点的坐标;
(2)指出圆心T一定在哪一条直线上运动;
(3)当点H在直线y=kx-1上,且⊙T的半径等于圆心T到原点距离的
| 2 |
分析:(1)根据过P的直线的解析式即可求出P(-1,0),而Q、P关于x轴对称,由此可求出Q点坐标.
(2)根据圆的对称性和垂径定理即可得出圆心必在x轴上运动.
(3)本题可分两种情况:分两种情况:①圆心T在x轴负半轴;②圆心T在x轴正半轴;解法一致.已知了圆的半径和圆心T到原点距离的倍数关系,通过连接TP构建直角三角形,可求出圆心的坐标和圆的半径.也就能求出M、N的坐标,然后根据M、N、C三点坐标即可求出抛物线的解析式也就能得出H点的坐标,然后将H点坐标代入直线的解析式中即可求出k的值.
(2)根据圆的对称性和垂径定理即可得出圆心必在x轴上运动.
(3)本题可分两种情况:分两种情况:①圆心T在x轴负半轴;②圆心T在x轴正半轴;解法一致.已知了圆的半径和圆心T到原点距离的倍数关系,通过连接TP构建直角三角形,可求出圆心的坐标和圆的半径.也就能求出M、N的坐标,然后根据M、N、C三点坐标即可求出抛物线的解析式也就能得出H点的坐标,然后将H点坐标代入直线的解析式中即可求出k的值.
解答:解:(1)y=kx-1交y于(0,-1)点,
∴P点的坐杯为(0,-1)
由Q与P关于原点对称,
∴Q点的坐标为(0,1).
(2)已知圆过M、N、P、Q四点,根据圆的对称性和垂径定理可知MN必为圆的直径,
因此圆心T在x轴上运动.
(3)当T在x轴负半轴上时,连接TP,则TP=
OT=
,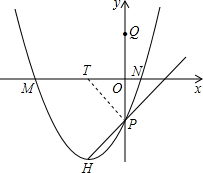
∴OT=1,△TOP为等腰直角三角形.
∴T(-1,0)
∵圆的半径TP=
,
∴M(-1-
,0),N(
-1,0).
设抛物线的解析式为y=a(x+1+
)(x+1-
),
已知抛物线过P(0,-1),
∴a(0+1+
)(0+1-
)=-1
∴a=1
∴y=x2+2x-1=(x+1)2-2
∴H(-1,-2),代入直线y=kx-1中,
得k=1,
同理可求得当T在x轴正半轴上时,k=-1.
因此k的值为±1.
∴P点的坐杯为(0,-1)
由Q与P关于原点对称,
∴Q点的坐标为(0,1).
(2)已知圆过M、N、P、Q四点,根据圆的对称性和垂径定理可知MN必为圆的直径,
因此圆心T在x轴上运动.
(3)当T在x轴负半轴上时,连接TP,则TP=
| 2 |
| 2 |

∴OT=1,△TOP为等腰直角三角形.
∴T(-1,0)
∵圆的半径TP=
| 2 |
∴M(-1-
| 2 |
| 2 |
设抛物线的解析式为y=a(x+1+
| 2 |
| 2 |
已知抛物线过P(0,-1),
∴a(0+1+
| 2 |
| 2 |
∴a=1
∴y=x2+2x-1=(x+1)2-2
∴H(-1,-2),代入直线y=kx-1中,
得k=1,
同理可求得当T在x轴正半轴上时,k=-1.
因此k的值为±1.
点评:本题主要考查了二次函数、一次函数以及圆的相关知识.难度适中.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 点Q与点P关于原点对称.抛物线y=ax2+bx+c经过点M、P、N,其顶点为H.
点Q与点P关于原点对称.抛物线y=ax2+bx+c经过点M、P、N,其顶点为H. 倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)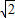 倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)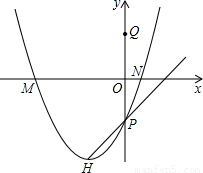
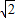 倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)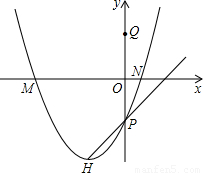
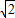 倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)