题目内容
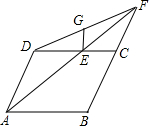已知：E是菱形ABCD的边DC上的一个点，AE交BC的延长线于F，EG∥AD交DF于G点，求证：EG=EC．
证明：∵EG∥AD，
∴
，
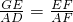∵四边形ABCD是菱形，
∴CE∥AB，AD=AB，
∴
，
∴
，
∴GE=EC．
分析：由四边形ABCD是菱形，即可得CE∥AB，AD=AB，又由EG∥AD，根据平行线分线段成比例定理，即可证得EG=EC．
点评：此题考查了平行线分线段成比例定理与菱形的性质．解题的关键是数形结合思想的应用．
∴
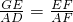，∵四边形ABCD是菱形，
∴CE∥AB，AD=AB，
∴
，∴
，∴GE=EC．
分析：由四边形ABCD是菱形，即可得CE∥AB，AD=AB，又由EG∥AD，根据平行线分线段成比例定理，即可证得EG=EC．
点评：此题考查了平行线分线段成比例定理与菱形的性质．解题的关键是数形结合思想的应用．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
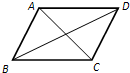8、如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）
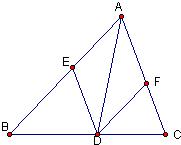22、已知，AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F．求证：四边形AEDF是菱形．
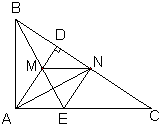17、已知，如图，△ABC中，∠BAC=90°，AD⊥BC于点D，BE平分∠ABC，交AD于点M，AN平分∠DAC，交BC于点N．
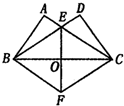28、已知：如图，△ABC和△DBC的顶点在BC边的同侧，AB=DC，AC=BD交于E，∠BEC的平分线交BC于O，延长EO到F，使EO=OF．求证：四边形BFCE是菱形．