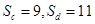题目内容
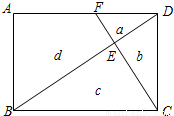
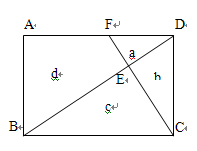
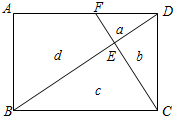 如图,BD、CF把矩形ABCD分成四块a、b、c、d,其中Sa=4,Sb=6,则Sc=?,Sd=?
如图,BD、CF把矩形ABCD分成四块a、b、c、d,其中Sa=4,Sb=6,则Sc=?,Sd=?
- A.Sc=8,Sd=10
- B.Sc=9,Sd=10
- C.Sc=12,Sd=14
- D.Sc=9,Sd=11
D
分析:根据等高的三角形的面积比等于边之比求出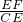 =
= ,证△DFE∽△BCE,得出
,证△DFE∽△BCE,得出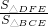 =
=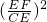 ,求出Sc=9,根据Sd=S矩形ABCD-Sa-Sb-Sc即可求出Sd.
,求出Sc=9,根据Sd=S矩形ABCD-Sa-Sb-Sc即可求出Sd.
解答:∵Sa=4,Sb=6,
又∵△DFE得边EF和△DEC的边CE上的高相等,
∴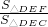 =
=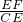 =
= ,
,
即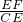 =
= ,
,
∵四边形ABCD是矩形,
∴AD∥BC,
∴△DFE∽△BCE,
∴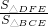 =
=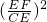 =
= ,
,
∵S△DFE=4,
∴S△BCE=9,
即Sc=9,
∵Sd=S矩形ABCD-Sa-Sb-Sc
=2(Sb+Sc)-Sa-Sb-sc
=Sb+Sc-Sa
=6+9-4
=11,
故选D.
点评:本题考查了矩形的性质,相似三角形的性质和判定,三角形的面积等知识点,注意:相似三角形的面积比等于相似比的平方.
分析:根据等高的三角形的面积比等于边之比求出
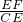 =
= ,证△DFE∽△BCE,得出
,证△DFE∽△BCE,得出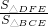 =
=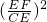 ,求出Sc=9,根据Sd=S矩形ABCD-Sa-Sb-Sc即可求出Sd.
,求出Sc=9,根据Sd=S矩形ABCD-Sa-Sb-Sc即可求出Sd.解答:∵Sa=4,Sb=6,
又∵△DFE得边EF和△DEC的边CE上的高相等,
∴
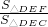 =
=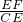 =
= ,
,即
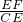 =
= ,
,∵四边形ABCD是矩形,
∴AD∥BC,
∴△DFE∽△BCE,
∴
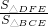 =
=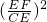 =
= ,
,∵S△DFE=4,
∴S△BCE=9,
即Sc=9,
∵Sd=S矩形ABCD-Sa-Sb-Sc
=2(Sb+Sc)-Sa-Sb-sc
=Sb+Sc-Sa
=6+9-4
=11,
故选D.
点评:本题考查了矩形的性质,相似三角形的性质和判定,三角形的面积等知识点,注意:相似三角形的面积比等于相似比的平方.

练习册系列答案
相关题目
 (2012•江西二模)如图,BD、CF把矩形ABCD分成四块a、b、c、d,其中Sa=4,Sb=6,则Sc=?,Sd=?( )
(2012•江西二模)如图,BD、CF把矩形ABCD分成四块a、b、c、d,其中Sa=4,Sb=6,则Sc=?,Sd=?( )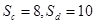 B.
B.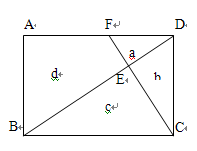
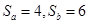 ,则
,则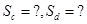
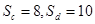 B.
B.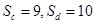
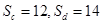 D.
D.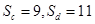
 ,则
,则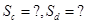
 B.
B.
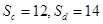 D.
D.