Question

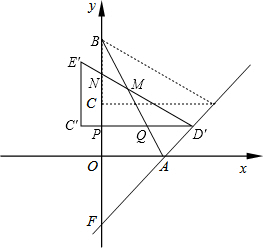
如图，把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中，使点E与点B重合，直角边OB、BC在y轴上．已知点D（4，2），过A、D两点的直线交y轴于点F．若△ECD沿DA方向以每秒

2

个单位长度的速度匀速平移，设平移的时间为t（秒），记△ECD在平移过程中某时刻为△E′C′D′，E′D′与AB交于点M，与y轴交于点N，C′D′与AB交于点Q，与y轴交于点P（注：平移过程中，点D′始终在线段DA上，且不与点A重合）．
（1）求直线AD的函数解析式；
（2）试探究在△ECD平移过程中，四边形MNPQ的面积是否存在最大值？若存在，求出这个最大值及t的取值；若不存在，请说明理由；
（3）以MN为边，在E′D′的下方作正方形MNRH，求正方形MNRH与坐标轴有两个公共点时t的取值范围．

Answer 1

（1）由题意A（2.0），
由D（4，2），
可得直线AD解析式：y=x-2；
（2）在△ECD平移过程中，四边形MNPQ的面积存在最大值，

理由如下：
由B（0，4），
可得直线AB解析式：y=-2x+4，
直线BD解析式：y=-

1

2

x+4，J（1，2）．
在△ECD平移t秒时，由∠CDF=45°，
可得D′（4-t，2-t），N（0，4-

3

2

t），
设直线E′D′解析式为：y=-

1

2

x+4-

3

2

t，
可得M（t，4-2t），
Q（

t+2

2

，2-t），P（0，2-t）
由△MQD′∽△BJD，得

S△MQD′

S△BJD

=(

3- 3 2 t

3

)2，
可得S_△MQD′=3(1-

1

2

t)2，
S_{梯形E′C′PN}=

1

2

t(2+2-

1

2

t)=-

1

4

t2+2t，
S_{四边形MNPQ}=S_{△E′C′D′-}S_△MQD′-S_{梯形E′C′PN}

=- 1 2 t2+t+1 =- 1 2 (t-1)2+ 3 2

∴当t=1时，S_最大=

3

2

；
（3）当点H在x轴上时，有M（t，4-2t）横纵坐标相等，
即t=4-2t，
∴t=

4

3

，
∴0＜t＜

4

3

．