题目内容
(1)如图1,线段AB与⊙O相切于点C,连接OA,OB,已知OA=OB=5cm,AB=8cm,求⊙O的半径.(2)已知:如图2,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,求证:AE=BD.
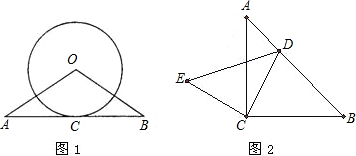
分析:(1)连接OC,则OC⊥AB.根据等腰三角形性质知AC=
AB.运用勾股定理可求半径OC;
(2)根据SAS证明△ACE≌△BCD即可.
| 1 |
| 2 |
(2)根据SAS证明△ACE≌△BCD即可.
解答:(1)解:连接OC.
∵AB与⊙O相切于点C,
∴OC⊥AB.(1分)
又∵OA=OB,
∴AC=BC=
AB=4cm (2分)
在Rt△AOC中,
OC=
=3cm,
∴半径为3cm.(3分)
(2)证明:∵∠ACB=∠DCE=90°,
∴∠BCD+∠DCA=90°,∠ACB+∠DCA=90°.
∴∠BCD=∠ACB.(4分)
又∵△ABC和△ECD都是等腰直角三角形,
∴BC=AC,DC=EC.(5分)
∴△BCD≌△ACE.(6分)
∴AE=BD.(7分)
∵AB与⊙O相切于点C,
∴OC⊥AB.(1分)
又∵OA=OB,
∴AC=BC=
| 1 |
| 2 |
在Rt△AOC中,
OC=
| OA2-AC2 |
∴半径为3cm.(3分)
(2)证明:∵∠ACB=∠DCE=90°,
∴∠BCD+∠DCA=90°,∠ACB+∠DCA=90°.
∴∠BCD=∠ACB.(4分)
又∵△ABC和△ECD都是等腰直角三角形,
∴BC=AC,DC=EC.(5分)
∴△BCD≌△ACE.(6分)
∴AE=BD.(7分)
点评:此题考查切线的性质、等腰三角形的性质、勾股定理、全等三角形的判定和性质等知识点,综合性较强.

练习册系列答案
相关题目


 (1996•山东)已知如图,相互线段a和b.求作:△ABC,使AB=AC=a,BC边上的中线等于b.(写出作法,保留作图痕迹,不要求证明)
(1996•山东)已知如图,相互线段a和b.求作:△ABC,使AB=AC=a,BC边上的中线等于b.(写出作法,保留作图痕迹,不要求证明)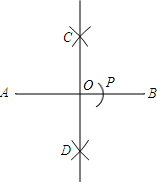 如图,画线段AB的垂直平分线交AB于点O,在这条垂直平分线上截取OC=OA,以A为圆心,AC为半径画弧于AB与点P,则线段AP与AB的比是( )
如图,画线段AB的垂直平分线交AB于点O,在这条垂直平分线上截取OC=OA,以A为圆心,AC为半径画弧于AB与点P,则线段AP与AB的比是( )