题目内容
已知:y=ax与![]() 两个函数图象交点为P(m,n),且m<n,m、n是关于x的一元二次方程kx2+(2k-7)x+k+3=0的两个不等实根,其中k为非负整数.
两个函数图象交点为P(m,n),且m<n,m、n是关于x的一元二次方程kx2+(2k-7)x+k+3=0的两个不等实根,其中k为非负整数.
(1)求k的值;
(2)求a、b的值;
(3)如果y=c(c≠0)与函数y=ax和y=![]() 交于A、B两点(点A在点B的左侧),线段AB=
交于A、B两点(点A在点B的左侧),线段AB=![]() ,求c的值.
,求c的值.
答案:
解析:
解析:
|
解:(1)△=(2k-7)2-4k(k+3)>0 k< ∵k为非负整数,∴k=0,1 ∵ ∴k=1 3分 (2)把k=1代入方程得x2-5x+4=0,解得x1=1,x2=4 ∵m<n ∴m=1,n=4 4分 把m=1,n=4代入 可得a=4,b=1 5分 (3)把y=c代入 可得A( 解得c1=2,c2=-8,经检验c1=2,c2=-8为方程的根 7分 ∴c1=2,c2=-8 |

练习册系列答案
相关题目
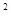 +bx+c与
+bx+c与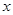 轴交于
轴交于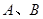 两点,若
两点,若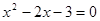 的两个实数根,与
的两个实数根,与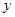 轴交于点
轴交于点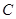 (0,3),
(0,3),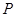 ,使
,使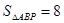 .
.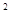 +bx+c与
+bx+c与 轴交于
轴交于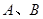 两点,若
两点,若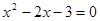 的两个实数根,与
的两个实数根,与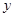 轴交于点
轴交于点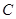 (0,3),
(0,3),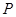 ,使
,使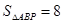 .
.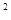 +bx+c与
+bx+c与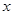 轴交于
轴交于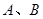 两点,若
两点,若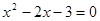 的两个实数根,与
的两个实数根,与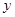 轴交于点
轴交于点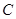 (0,3),
(0,3),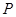 ,使
,使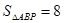 .
. +bx+c与
+bx+c与 轴交于
轴交于 两点,若
两点,若 的两个实数根,与
的两个实数根,与 轴交于点
轴交于点 (0,3),
(0,3),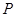 ,使
,使 .
.