��Ŀ����
����Ŀ����֪ʶ���ӡ� ��������ʽ���������и�ʽ�ķ������ʽ��ˣ�������ǵĻ������и�ʽ����ô����������ʽ�������������ʽ��
���磺 ![]() ����������ʽ��
����������ʽ�� ![]() ��1��
��1�� ![]() ����������ʽ��1+
����������ʽ��1+ ![]() ��
��
��ĸ����������ĸ�������ֳơ���������ĸ����Ҳ���ǰѷ�ĸ�еĸ��Ż�ȥ��ָ�����������ʽ�з�ĸ�и��ţ���ôͨ�������ӡ���ĸͬ���Է�ĸ����������ʽ���ﵽ��ȥ��ĸ�и��ŵ�Ŀ�ģ��磺![]() =
= ![]() =
= ![]() ��1��
��1�� ![]() =
= ![]() =
= ![]() ��
�� ![]() ��
��
��1����֪ʶ���⡿ ��գ�2 ![]() ����������ʽ����
����������ʽ����
ֱ��д�����и�ʽ��ĸ�������Ľ����
�� ![]() =����
=���� ![]() = ��
= ��
��2�����������á� ���㣺 ![]() +
+ ![]() +
+ ![]() +��+
+��+ ![]() ��
��
���𰸡�
��1��![]() ��
�� ![]() ��
�� ![]() ��3
��3 ![]() ��
�� ![]()
��2��ԭʽ= 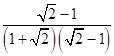 +
+  +
+ 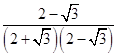 +��+
+��+  ��
��
= ![]() ��1+
��1+ ![]() ��
�� ![]() +2��
+2�� ![]() +��+
+��+ ![]() ��
�� ![]() ��
��
= ![]() ��1��
��1��
���������⣺��1����2 ![]() ��
�� ![]() =2x��
=2x��
��2 ![]() ����������ʽ��
����������ʽ�� ![]() ��
��
���Դ��ǣ� ![]() ��
��
�� ![]() =
= ![]() =
= ![]() ��
�� ![]() ��
��
�� ![]() =
= ![]() =3
=3 ![]() ��
�� ![]() ��
��
���Դ��ǣ��� ![]() ��
�� ![]() ��3
��3 ![]() ��
�� ![]() ��
��

��ϰ��ϵ�д�
�����Ŀ