题目内容
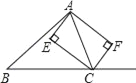
【题目】已知：如图，CE、CF分别是△ABC的内外角平分线，过点A作CE、CF的垂线，垂足分别为E、F．
（1）求证：四边形AECF是矩形；
（2）当△ABC满足什么条件时，四边形AECF是正方形？
【答案】（1）见解析；（2）当△ABC满足∠ACB=90°时，四边形AECF是正方形
【解析】（1）求出∠ECF=90°=∠E=∠F，即可推出答案；
（2）∠ACB=90°，推出∠ACE=∠EAC=45°，AE=CE即可．
(1)证明：∵CE、CF分别是△ABC的内外角平分线，
∴
∵AE⊥CE，AF⊥CF，
∴
∴四边形AECF是矩形.
(2)答：当△ABC满足
时，四边形AECF是正方形，
理由是：∵
∵
∴
∴AE=CE，
∵四边形AECF是矩形，
∴四边形AECF是正方形.
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
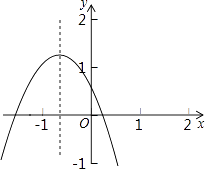
【题目】初三数学课本上，用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣15.5 | ﹣5 | ﹣3.5 | ﹣2 | ﹣3.5 | … |
根据表格上的信息回答问题：该二次函数y=ax2+bx+c在x=3时，y= ．
