题目内容
【题目】如图①是一张矩形纸片![]() ,
, ![]() ,
, ![]() .在边
.在边![]() 上取一点
上取一点![]() ,在边
,在边![]() 上取一点
上取一点![]() ,将纸片沿
,将纸片沿![]() 折叠,使
折叠,使![]() 与
与![]() 交于点
交于点![]() ,得到
,得到![]() ,如图②所示.
,如图②所示.
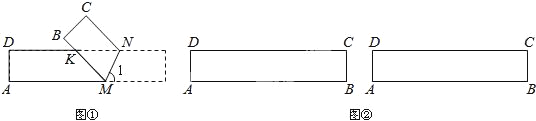
(1)若![]() ,求
,求![]() 的度数.
的度数.
(2) ![]() 的面积能否小于
的面积能否小于![]() ?若能,求出此时
?若能,求出此时![]() 的度数;若不能,试说明理由.
的度数;若不能,试说明理由.
(3)如何折叠能够使![]() 的面积最大?请你画图探究可能出现的情况,求出最大值.
的面积最大?请你画图探究可能出现的情况,求出最大值.
【答案】(1) 40°.(2) △MNK的面积不能小于![]() ;理由见解析;(3)1.3
;理由见解析;(3)1.3
【解析】
试题分析:(1)证明∠MKN=∠KMA;证明∠KMN=∠1=70°,即可解决问题.
(2)如图1,作辅助线;证明MK>1;证明NK=MK>1,运用三角形的面积公式即可解决问题.
(3)如图2,证明MK=MQ(设为λ),得到AM=5-λ;列出关于λ的方程(5-λ)2+12=λ2,求出λ即可解决问题.
试题解析:(1)如图1,∵四边形ABCD为矩形,
∴DN∥AM,∠MKN=∠KMA;
由题意得:∠KMN=∠1=70°,
∴∠KMA=180°-140°=40°,
∴∠MKN=40°.
(2)△MNK的面积不能小于![]() ;理由如下:
;理由如下:
如图1,过点M作MP⊥KN;则MP=1;
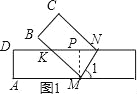
由题意得MK>1,∠KMN=∠1;
∵KN∥AM,
∴∠KNM=∠1,∠KMN=∠KNM,
∴NK=MK>1,
∴S△MNK=![]() NK×MP>
NK×MP>![]() .
.
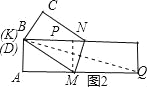
(3)如图2,当点B与点D重合时,△MNK的面积最大;
由题意得:MK=MQ(设为λ),则AM=5-λ;
由勾股定理得:(5-λ)2+12=λ2,
解得:λ=2.6;由(1)知:
NK=MK=2.6,MP=1,
∴S△MNK=![]() NK×MP =1.3.
NK×MP =1.3.

练习册系列答案
相关题目

