题目内容
已知:如图,矩形ABCD中AB=4,AD=12,点P是线段AD上的一动点(点P不与点A,D重合),点Q是直线CD上的一点,且PQ⊥BP,连接BQ,设AP=x,DQ=y
(1)求证:△ABP∽△DPQ.
(2)求y与x的函数关系式,并写出自变量x的取值范围.
(3)并求出当y取何值,△ABP∽△PBQ.
(4)若点Q在DC的延长线上,则x的取值范围________.(不必写出过程).

证明:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠ABP+∠APB=90°,∠PQD+∠QPD=90°,
∵PQ⊥BP,
∴∠DPQ+∠APB=90°
∴∠APB=∠PQD,
∴△ABP∽△DPQ;
(2)∵△ABP∽△DPQ.
∴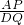 =
= ,
,
∵AB=4,AD=12
∴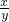 =
= ,即y=3x-
,即y=3x-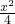 .
.
∵AP与AD不重合,
∴0<x<12;
答:y与x的函数关系式为:y=3x-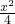 ;
;
自变量x的取值范围是:0<x<12;
(3)假设△ABP∽△PBQ,
则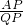 =
=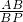 ,即
,即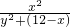 =
=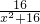 ,
,
将y=3x-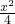 代入上式,解得x=6.
代入上式,解得x=6.
将x=6代入y=3x-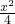 ,解得y=9.
,解得y=9.
答:当y=9时.△ABP∽△PBQ;
(4)∵Q在DC的延长线上,
∴y>4,即3x-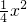 >4,
>4,
解此方程得6-2 <x<6+2
<x<6+2 .
.
故答案为:6-2 <x<6+2
<x<6+2 .
.
分析:(1)根据四边形ABCD是矩形和PQ⊥BP,利用两组对应角相等即可求证△ABP∽△DPQ.
(2)根据△ABP∽△DPQ.利用其对应边成比例,将已知数值代入即可得出y与x的函数关系式.根据(点P不与点A,D重合),即可求出自变量x的取值范围.
(3)假设△ABP∽△PBQ.利用其对应边成比例,解得x的值,然后将x的值代入y=3x-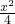 即可.
即可.
(4)根据Q在DC的延长线上可知y>4,即3x-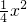 >4,解此方程即可得出则x的取值范围.
>4,解此方程即可得出则x的取值范围.
点评:此题涉及到相似三角形的判定与性质,矩形的性质,勾股定理,函数等多个知识点的理解和掌握,综合性很强,难度较大,尤其是解此方程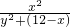 =
=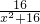 ,总之此题是一道难题.
,总之此题是一道难题.
∴∠A=∠D=90°,
∴∠ABP+∠APB=90°,∠PQD+∠QPD=90°,
∵PQ⊥BP,
∴∠DPQ+∠APB=90°
∴∠APB=∠PQD,
∴△ABP∽△DPQ;
(2)∵△ABP∽△DPQ.
∴
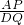 =
= ,
,∵AB=4,AD=12
∴
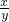 =
= ,即y=3x-
,即y=3x-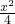 .
.∵AP与AD不重合,
∴0<x<12;
答:y与x的函数关系式为:y=3x-
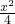 ;
;自变量x的取值范围是:0<x<12;
(3)假设△ABP∽△PBQ,
则
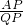 =
=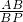 ,即
,即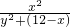 =
=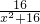 ,
,将y=3x-
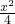 代入上式,解得x=6.
代入上式,解得x=6.将x=6代入y=3x-
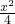 ,解得y=9.
,解得y=9.答:当y=9时.△ABP∽△PBQ;
(4)∵Q在DC的延长线上,
∴y>4,即3x-
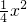 >4,
>4,解此方程得6-2
 <x<6+2
<x<6+2 .
.故答案为:6-2
 <x<6+2
<x<6+2 .
.分析:(1)根据四边形ABCD是矩形和PQ⊥BP,利用两组对应角相等即可求证△ABP∽△DPQ.
(2)根据△ABP∽△DPQ.利用其对应边成比例,将已知数值代入即可得出y与x的函数关系式.根据(点P不与点A,D重合),即可求出自变量x的取值范围.
(3)假设△ABP∽△PBQ.利用其对应边成比例,解得x的值,然后将x的值代入y=3x-
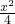 即可.
即可.(4)根据Q在DC的延长线上可知y>4,即3x-
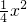 >4,解此方程即可得出则x的取值范围.
>4,解此方程即可得出则x的取值范围.点评:此题涉及到相似三角形的判定与性质,矩形的性质,勾股定理,函数等多个知识点的理解和掌握,综合性很强,难度较大,尤其是解此方程
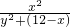 =
=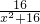 ,总之此题是一道难题.
,总之此题是一道难题. 
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
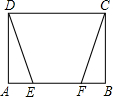 已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF.
已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF.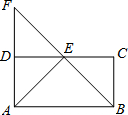 19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.
19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.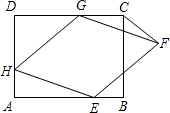 上,AH=2,连接CF.
上,AH=2,连接CF.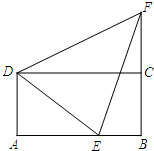 已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF.
已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF.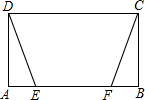 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.