题目内容
(1)计算: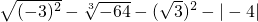
(2)先化简再求值:4(m+1)2-(2m+5)(2m-5).其中m=-3;
(3)因式分解:-a+2a2-a3.
解:(1)原式=3+4-3-4=0;
(2)4(m+1)2-(2m+5)(2m-5),
=4(m2+2m+1)-4m2-25,
=4m2+8m+4-4m2-25,
=8m-21,
当m=-3时,原式=8m-21=8×(-3)-21,
=-45;
(3)-a+2a2-a3,
=-a(1-2a+a2),
=-a(1-a)2.
分析:(1)题先按运算顺序把整式化简,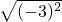 开方应注意符号问题,
开方应注意符号问题,
(2)题应注意先化简再求值,去括号后,合并同类项;
(3)题应首先提取公因式-a,再利用完全公式分解因式.
点评:此题考查了实数的运算,特别是根式的开方问题,整式的运算应注意先化简再求值,因式分解应先提取公因式后,在分析能否继续因式分解.
(2)4(m+1)2-(2m+5)(2m-5),
=4(m2+2m+1)-4m2-25,
=4m2+8m+4-4m2-25,
=8m-21,
当m=-3时,原式=8m-21=8×(-3)-21,
=-45;
(3)-a+2a2-a3,
=-a(1-2a+a2),
=-a(1-a)2.
分析:(1)题先按运算顺序把整式化简,
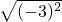 开方应注意符号问题,
开方应注意符号问题,(2)题应注意先化简再求值,去括号后,合并同类项;
(3)题应首先提取公因式-a,再利用完全公式分解因式.
点评:此题考查了实数的运算,特别是根式的开方问题,整式的运算应注意先化简再求值,因式分解应先提取公因式后,在分析能否继续因式分解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目