题目内容
我校初三学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分排列名次,在规定的时间内踢100个以上(含100)的为优秀,甲班和乙班5名学生的比赛成绩如下表(单位:个):
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙 | 89 | 100 | 95 | 119 | 97 | 500 |
(1)计算两班的优秀率;
(2)求两班比赛成绩的方差;
(3)根据以上2条信息,你认为应该把冠军杯给哪一个班级?简述理由.
解:(1)甲班的优秀率=3÷5×100%=60%,乙班的优秀率=2÷5×100%=40%;
(2)甲的平均数为:100+98+110+89+103)÷5=100,
S 甲2=[(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2]÷5=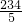 ;
;
乙的平均数为:(89+100+95+119+97)÷5=100,
S 乙2=[(89-100)2+(100-100)2+(95-100)2+(97-100)2+(119-100)2]÷5=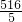 ,
,
∵S 甲2<S 乙2,∴甲稳定;
甲班极差=110-89=21,
乙班极差=119-89=30,
则21<30,
故甲稳定.
(3)冠军应发给甲.
因为甲班的优秀率比乙班高;甲班的中位数比乙班高;甲班的方差比乙班低,比较稳定,综合评定甲班比较好.
分析:(1)先求出每个班优秀的人数,再求得优秀率;
(2)利用极差定义以及方差公式求得两个班的方差,根据方差越小成绩越稳定,进行判断;
(3)由优秀率、中位数、方差进行比较,再进行判断.
点评:本题考查了中位数、平均数和方差的定义与意义.它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
(2)甲的平均数为:100+98+110+89+103)÷5=100,
S 甲2=[(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2]÷5=
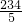 ;
;乙的平均数为:(89+100+95+119+97)÷5=100,
S 乙2=[(89-100)2+(100-100)2+(95-100)2+(97-100)2+(119-100)2]÷5=
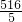 ,
,∵S 甲2<S 乙2,∴甲稳定;
甲班极差=110-89=21,
乙班极差=119-89=30,
则21<30,
故甲稳定.
(3)冠军应发给甲.
因为甲班的优秀率比乙班高;甲班的中位数比乙班高;甲班的方差比乙班低,比较稳定,综合评定甲班比较好.
分析:(1)先求出每个班优秀的人数,再求得优秀率;
(2)利用极差定义以及方差公式求得两个班的方差,根据方差越小成绩越稳定,进行判断;
(3)由优秀率、中位数、方差进行比较,再进行判断.
点评:本题考查了中位数、平均数和方差的定义与意义.它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
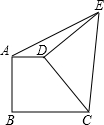 如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是
如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是
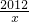 中自变量x的取值范围是
中自变量x的取值范围是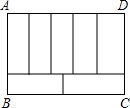 如图所示,周长为34的长方形ABCD被分成7个大小完全一样的小长方形,则每个小长方形的面积为
如图所示,周长为34的长方形ABCD被分成7个大小完全一样的小长方形,则每个小长方形的面积为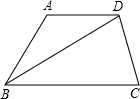 如图,梯形ABCD中,AD∥BC,AB=AD,BC=BD,∠A=120°,则∠ADC=________°.
如图,梯形ABCD中,AD∥BC,AB=AD,BC=BD,∠A=120°,则∠ADC=________°.