题目内容
某新建小区要在一块等边三角形的公共区域内修建一个圆形花坛．（1）若要使花坛面积最大，请你在这块公共区域（如图）内确定圆形花坛的圆心P；
（2）若这个等边三角形的边长为18米，请计算出花坛的面积．
分析：由题意可知三角形为正三角形，设计方案可根据内切圆性质及正三角形的性质，在三角形内作内切圆使圆形花坛面积最大，然后有圆的性质求出内切圆的半径，从而求出面积．
解答：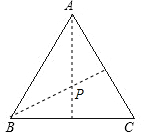
解：（1）要使花坛面积最大，因三角形为等边三角形，在△ABC内作一个内切圆，则此圆面积最大，点P为角平分线的交点．
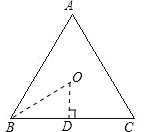
（2）如图，Rt△BOD中，BD=9米，∠OBD=30°
∴tan30°=
，
∴OD=BD•tan30°=9×
=3
，
∴花坛面积为π•（3
）2=27π（米2）．
解：（1）要使花坛面积最大，因三角形为等边三角形，在△ABC内作一个内切圆，则此圆面积最大，点P为角平分线的交点．（2）如图，Rt△BOD中，BD=9米，∠OBD=30°
∴tan30°=
| OD |
| BD |
∴OD=BD•tan30°=9×
| ||
| 3 |
| 3 |
∴花坛面积为π•（3
| 3 |
点评：此题为设计性问题，其实质是考查正三角形及内切圆的性质，同时也考查了圆的性质和简单的计算．
练习册系列答案
相关题目
某新建小区要在一块等边三角形内修建一个圆形花坛．
某新建小区要在一块等边三角形的公共区域内修建一个圆形花坛．
某新建小区要在一块等边三角形内修建一个圆形花坛．