题目内容
如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴的正半轴上,且AB=OC.(1)求点C的坐标;
(2)求这个二次函数的解析式;
(3)自变量x在什么范围内时,y随x的增大而增大?何时,y随x的增大而减少?

【答案】分析:(1)根据题目所给的信息可以知道OC=AB=5,点C在y轴上可以写出点C的坐标.
(2)二次函数图象经过点A、B、C;这三个点的坐标已知,根据三点法确定这一二次函数解析式.
(3)由二次函数性质可以知道,对于开口向下的二次函数图象,对称轴左边y随x的增大而增大,在对称轴右面y随x的增大而减少.
解答:解:(1)有题目可以知道OC=AB=5,
所以点C的坐标为(0,5);
(2)设二次函数解析式为:y=kx2+bx+c,
且有此二次函数图象过点:A(-1,0)、B(4,0)、C(0,5),
把三点代入原函数解析式得出:
k=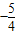 ,b=
,b=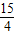 ,c=5;
,c=5;
所以这个二次函数的解析式为:y= ;
;
(3)由二次函数图象性质可以知道:
对于开口向下的二次函数图象,在对称轴左边y随x的增大而增大,在对称轴右面y随x的增大而减少.
此二次函数的对称轴是x=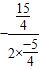 =
= ,
,
答:自变量x< 时,y随x的增大而增大,自变量x>
时,y随x的增大而增大,自变量x> 时,y随x的增大而减少.
时,y随x的增大而减少.
点评:本题主要考查了二次函数解析式的解法,以及二次函数图象的性质.
(2)二次函数图象经过点A、B、C;这三个点的坐标已知,根据三点法确定这一二次函数解析式.
(3)由二次函数性质可以知道,对于开口向下的二次函数图象,对称轴左边y随x的增大而增大,在对称轴右面y随x的增大而减少.
解答:解:(1)有题目可以知道OC=AB=5,
所以点C的坐标为(0,5);
(2)设二次函数解析式为:y=kx2+bx+c,
且有此二次函数图象过点:A(-1,0)、B(4,0)、C(0,5),
把三点代入原函数解析式得出:
k=
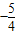 ,b=
,b=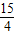 ,c=5;
,c=5;所以这个二次函数的解析式为:y=
 ;
;(3)由二次函数图象性质可以知道:
对于开口向下的二次函数图象,在对称轴左边y随x的增大而增大,在对称轴右面y随x的增大而减少.
此二次函数的对称轴是x=
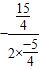 =
= ,
,答:自变量x<
 时,y随x的增大而增大,自变量x>
时,y随x的增大而增大,自变量x> 时,y随x的增大而减少.
时,y随x的增大而减少.点评:本题主要考查了二次函数解析式的解法,以及二次函数图象的性质.

练习册系列答案
相关题目
 为(4,0),点C在y轴的正半轴上,且AB=OC.
为(4,0),点C在y轴的正半轴上,且AB=OC. 为(4,0),点C在y轴的正半轴上,且AB=OC.
为(4,0),点C在y轴的正半轴上,且AB=OC. ),点B的坐标为(
),点B的坐标为( ),点C在y轴的正半轴上,且AB=OC.
),点C在y轴的正半轴上,且AB=OC.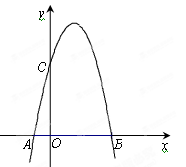
 ),点B的坐标为(
),点B的坐标为( ),点C在y轴的正半轴上,且AB=OC.
),点C在y轴的正半轴上,且AB=OC.