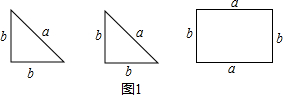题目内容
有3张纸片,如图1,其中①、②是同样的等腰直角三角形,③是矩形(长方形),各边长度如图所示(显然a>b).
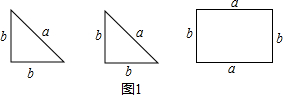
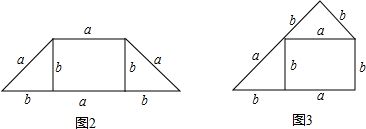
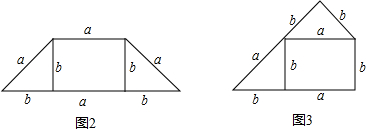
用图1中的纸片分别拼成图2、图3的形状不同的四边形.
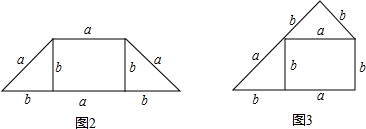
(1)分别记图2、图3的图形周长为m,n,求m,n(用a,b的式子表示),并比较m,n的大小;
(2)用图1中的全部纸片再拼成与图2、图3形状不同的两个四边形,并分别求出它们的周长.
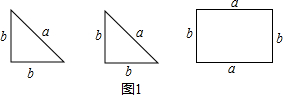
用图1中的纸片分别拼成图2、图3的形状不同的四边形.

(1)分别记图2、图3的图形周长为m,n,求m,n(用a,b的式子表示),并比较m,n的大小;
(2)用图1中的全部纸片再拼成与图2、图3形状不同的两个四边形,并分别求出它们的周长.
分析:(1)根据图形的中各边长即可得出m,n的长度,进而得出m,n的大小关系;
(2)根据图中已知图片以及各边长即可得出拼凑图形.
(2)根据图中已知图片以及各边长即可得出拼凑图形.
解答:(1)解:m=a+a+a+b+a+b=4a+2b,
n=a+b+b+b+a+b=2a+4b;
∵a>b,
∴m>n,
(2)解:
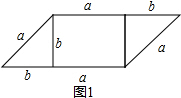
m=a+a+b+a+a+b=4a+2b,

n=b+b+a+b+a+b=2a+4b.
n=a+b+b+b+a+b=2a+4b;
∵a>b,
∴m>n,
(2)解:

m=a+a+b+a+a+b=4a+2b,

n=b+b+a+b+a+b=2a+4b.
点评:此题主要考查了图形的剪拼以及列代数式和合并同类项,根据图形各边长得出拼凑图形是解题关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目