题目内容
【题目】小明同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先画出了如图的四边形ABCD,并写出了如下不完整的已知和求证. 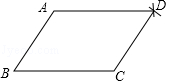
(1)在方框中填空,以补全已知和求证; 已知:如图,在四边形ABCD中,BC=AD, .
求证:四边形ABCD是 .
(2)写出证明过程:
【答案】
(1)AB=CD;平行四边形
(2)证明:连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABC D是平行四边形.
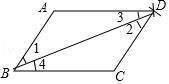
【解析】(1)题设作为已知条件,结论作为求证即可解决问题;(2)连接BD,只要证明△ABD≌△CDB.推出∠1=∠2,∠3=∠4.推出AB∥CD,AD∥CB即可;
【考点精析】掌握平行四边形的判定是解答本题的根本,需要知道两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目