题目内容
先阅读,再分解因式:
把
-2ab+
-
因式分解.
解:原式=(
-2ab+
)-
=(a-b
-
=(a-b+c)(a-b-c).
请你仔细阅读上述解法后,把下面的多项式因式分解:
(1)4
-4xy+
-
;
(2)1-
-
+2mn.
把
| a | 2 |
| b | 2 |
| c | 2 |
解:原式=(
| a | 2 |
| b | 2 |
| c | 2 |
=(a-b
| ) | 2 |
| c | 2 |
请你仔细阅读上述解法后,把下面的多项式因式分解:
(1)4
| x | 2 |
| y | 2 |
| a | 2 |
(2)1-
| m | 2 |
| n | 2 |
分析:(1)首先将原式进行分组得到原式=(2x-y) 2-a2,再利用公式法分解因式即可.
(2)首先将原式进行分组得到原式=1-(m-n) 2,再利用公式法分解因式即可.
(2)首先将原式进行分组得到原式=1-(m-n) 2,再利用公式法分解因式即可.
解答:解:(1)4x2-4xy+4y2-a2
=(2x-y) 2-a2
=(2x-y+a)(2x-y-a);
(2)1-
-
+2mn
=1-(m-n) 2
=(1-m+n)(1+m-n).
=(2x-y) 2-a2
=(2x-y+a)(2x-y-a);
(2)1-
| m | 2 |
| n | 2 |
=1-(m-n) 2
=(1-m+n)(1+m-n).
点评:此题主要考查了利用分组分解法分解因式,解题关键是首先把多项式正确的分组,然后利用公式法即可解决问题,注意分解因式要彻底.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
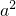 -2ab+
-2ab+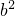 -
-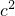 因式分解.
因式分解.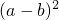 -
-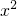 -4xy+
-4xy+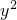 -
-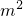 -
-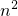 +2mn.
+2mn.