Question

如图，n+1个上底、两腰长皆为1，下底长为2的等腰梯形的下底均在同一直线上，设四边形P₁M₁N₁N₂面积为S₁，四边形P₂M₂N₂N₃的面积为S₂，…，四边形P_nM_nN_nN_n+1的面积为S_n，通过逐一计算S₁，S₂，…，可得S_n=　         　．

 

Answer 1

【答案】

【解析】

试题分析：如图，根据题意，小梯形中，

过D作DE∥BC交AB于E，

∵上底、两腰长皆为1，下底长为2，

∴AE=2﹣1=1，

∴△AED是等边三角形，

∴高h=1×sin60°=，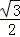

S_梯形=×（1+2）×=，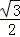

设四边形P_nM_nN_nN_n+1的上方的小三角形的高为x，

根据小三角形与△AM_nN_n相似，AN_n=2n，

由相似三角形对应边上高的比等于相似比，可知，

解得x==，

∴S_n=S_梯形﹣×1×，

=﹣．

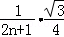考点：相似三角形的判定与性质；等腰梯形的性质．510329

点评：解答本题关键在于看出四边形P_nM_nN_nN_n+1的面积等于一个小梯形的面积减掉它上方的小三角形的面积，而小三角形的面积可以利用相似三角形的性质求出，此题也就解决了．