题目内容
阅读材料:如果一元二次方程ax2+bx+c=0(a≠0)的两个实数根分别是x1、x2,那么x1+x2=-
,x1•x2=
.借助该材料完成下列各题:
(1)若x1、x2是方程x2-4x+
=0的两个实数根,x1+x2=______;x1•x2=______.
(2)若x1、x2是方程2x2+6x-3=0的两个实数根,
+
=______;
+
=______.
(3)若x1、x2是关于x的方程x2-(m-3)x+m+8=0的两个实数根,且
+
=13,求m的值.
| b |
| a |
| c |
| a |
(1)若x1、x2是方程x2-4x+
| 5 |
(2)若x1、x2是方程2x2+6x-3=0的两个实数根,
| 1 |
| x1 |
| 1 |
| x2 |
| x | 21 |
| x | 22 |
(3)若x1、x2是关于x的方程x2-(m-3)x+m+8=0的两个实数根,且
| x | 21 |
| x | 22 |
(1)∵x1、x2是方程x2-4x+
=0的两个实数根,
∴x1+x2=-
=4,x1•x2=
=
;
故答案是:4,
;
(2)∵x1、x2是方程2x2+6x-3=0的两个实数根,
∴x1+x2=
=3,x1•x2=
=-
,
∴
+
=
=
=-2,
+
=(x1+x2)2-2x1•x2=32-2×(-
)=12.
故答案是:-2,12;
(3)∵关于x的方程x2-(m-3)x+m+8=0有两个实数根,
∴△=(m-3)2-4(m+8)≥0,即m≥5+4
,或m≤5-4
∵x1、x2是关于x的方程x2-(m-3)x+m+8=0的两个实数根,
∴x1+x2=m-3,x1•x2=m+8,
∴
+
=(x1+x2)2-2x1•x2=13,即(m-3)2-2(m+8)=13,
解得,m=-2或m=10.
即m的值是-2或10.
| 5 |
∴x1+x2=-
| -4 |
| 1 |
| ||
| 1 |
| 5 |
故答案是:4,
| 5 |
(2)∵x1、x2是方程2x2+6x-3=0的两个实数根,
∴x1+x2=
| 6 |
| 2 |
| -3 |
| 2 |
| 3 |
| 2 |
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1•x2 |
| 3 | ||
-
|
| x | 21 |
| x | 22 |
| 3 |
| 2 |
故答案是:-2,12;
(3)∵关于x的方程x2-(m-3)x+m+8=0有两个实数根,
∴△=(m-3)2-4(m+8)≥0,即m≥5+4
| 3 |
| 3 |
∵x1、x2是关于x的方程x2-(m-3)x+m+8=0的两个实数根,
∴x1+x2=m-3,x1•x2=m+8,
∴
| x | 21 |
| x | 22 |
解得,m=-2或m=10.
即m的值是-2或10.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,x1x2=
,x1x2= .∵
.∵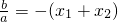
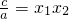 ,∴
,∴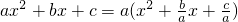 =a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).
=a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2). ,x1x2=
,x1x2= .
.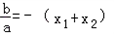
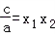 ,
,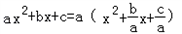 =a[x2﹣(x1+x2)x+x1x2]=a(x﹣x1)(x﹣x2).
=a[x2﹣(x1+x2)x+x1x2]=a(x﹣x1)(x﹣x2).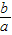 ,x1x2=
,x1x2=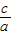 .∵
.∵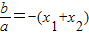
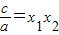 ,∴
,∴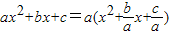 =a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).
=a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).