题目内容
(2001•河北)某化工材料经销公司购进了一种化工原料共7000千克,购进价格为每千克30元.物价部门规定销售单价不得高于每千克70元,也不得低于30元.市场调查发现:单价为70元时,日均销售60千克;单价每降低1元,日均多销售出2千克.在销售过程中,每天还要支出其他费用500元(天数不足一天时,按整天计算).设销售单价为x元,日均获利为y元.(1)求y与x的二次函数关系式,并指出自变量x的取值范围;
(2)将(1)中所求出的二次函数配方成y=a(x+
 )2+
)2+ 的形式.写出顶点坐标,并在图中画出草图;观察图象,指出单价定为多少时日均获利最多是多少?
的形式.写出顶点坐标,并在图中画出草图;观察图象,指出单价定为多少时日均获利最多是多少?(3)若将这种化工原料全部售出,比较日均获利最多和销售单价最高这两种销售方式,哪一种获总利较多,多多少?
【答案】分析:(1)日利润=每千克的利润×日销售量-杂支.每千克利润为(x-30)元,每千克降低(70-x)元,日均多销售出2(70-x)千克,日均销售量为[60+2(70-x)]千克,杂支为500元,所以得函数关系式.根据题意30≤x≤70;
(2)运用配方法配成顶点式,得顶点坐标,通过画图观察图象的最高点位置就是获利最多,此时对应的x的值即为定价;
(3)销售单价最高即是每千克70元销售,日销售量60千克,全部售出需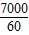 天,计算此时的利润,与日均获利最多的销售方式比较,即得结论.
天,计算此时的利润,与日均获利最多的销售方式比较,即得结论.
解答: 解:(1)设销售单价为x元,
解:(1)设销售单价为x元,
则每千克降低(70-x)元,日均多销售出2(70-x)千克,
日均销售量为[60+2(70-x)]千克,每千克获利为(x-30)元.
故y=(x-30)[60+2(70-x)]-500=-2x2+260x-6500(30≤x≤70);
(2)∵函数y=-2x2+260x-6500可化为y=-2(x-65)2+1950的形式,
∴顶点坐标为(65,1950),
画出草图:
经观察可知,当单价定为65元时,日均获利最多,为1950元;
(3)当日均获利最多时:
单价为65元,日均销售60+2×(70-65)=70千克,
将这种化工原料全部销售完需7000÷70=100天,
总获利为1950×100=195000元,
当销售单价最高时,
单价为70元,日均销售60千克,
将这种化工原料全部销售完需 天,
天,
获总利为(70-30)×7000-117×500=221500元,
221500-195000=26500元,故销售单价最高时获总利较多,且多获利26500元.
点评:此题的难度在比较两种不同的销售方式的利润,涉及销售时间的问题,这点应该注意.
(2)运用配方法配成顶点式,得顶点坐标,通过画图观察图象的最高点位置就是获利最多,此时对应的x的值即为定价;
(3)销售单价最高即是每千克70元销售,日销售量60千克,全部售出需
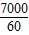 天,计算此时的利润,与日均获利最多的销售方式比较,即得结论.
天,计算此时的利润,与日均获利最多的销售方式比较,即得结论.解答:
 解:(1)设销售单价为x元,
解:(1)设销售单价为x元,则每千克降低(70-x)元,日均多销售出2(70-x)千克,
日均销售量为[60+2(70-x)]千克,每千克获利为(x-30)元.
故y=(x-30)[60+2(70-x)]-500=-2x2+260x-6500(30≤x≤70);
(2)∵函数y=-2x2+260x-6500可化为y=-2(x-65)2+1950的形式,
∴顶点坐标为(65,1950),
画出草图:
经观察可知,当单价定为65元时,日均获利最多,为1950元;
(3)当日均获利最多时:
单价为65元,日均销售60+2×(70-65)=70千克,
将这种化工原料全部销售完需7000÷70=100天,
总获利为1950×100=195000元,
当销售单价最高时,
单价为70元,日均销售60千克,
将这种化工原料全部销售完需
 天,
天,获总利为(70-30)×7000-117×500=221500元,
221500-195000=26500元,故销售单价最高时获总利较多,且多获利26500元.
点评:此题的难度在比较两种不同的销售方式的利润,涉及销售时间的问题,这点应该注意.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

