题目内容
经过点(4,0)且与坐标轴围成的三角形面积为4的直线的表达式是
y=-
x+2或y=
x-2
| 1 |
| 2 |
| 1 |
| 2 |
y=-
x+2或y=
x-2
.| 1 |
| 2 |
| 1 |
| 2 |
分析:首先设直线的解析式是y=kx+b(k≠0),则与y轴的交点为(0,b)根据所围成的三角形的面积和经过点(4,0)可求得k和b的值.
解答:解:设一次函数为y=kx+b(k≠0).则与y轴的交点为(0,b)
S△=
×4×|b|=4,得|b|=2,∴b=±2;
当b=2时,函数为:y=kx+6,
∵函数的图象经过点(4,0),得:0=4k+2得到k=-
∴所求的一次函数的解析式为:y=-
x+2;
b=-6时,函数为:y=kx-6
∵函数的图象经过点(4,0),
得:0=4k-2,得到k=
∴所求的一次函数的解析式为:y=
x-2.
综上所述,所求的一次函数的解析式为:y=-
x+2或y=
x-2.
故答案是:y=-
x+2或y=
x-2.
S△=
| 1 |
| 2 |
当b=2时,函数为:y=kx+6,
∵函数的图象经过点(4,0),得:0=4k+2得到k=-
| 1 |
| 2 |
∴所求的一次函数的解析式为:y=-
| 1 |
| 2 |
b=-6时,函数为:y=kx-6
∵函数的图象经过点(4,0),
得:0=4k-2,得到k=
| 1 |
| 2 |
∴所求的一次函数的解析式为:y=
| 1 |
| 2 |
综上所述,所求的一次函数的解析式为:y=-
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:y=-
| 1 |
| 2 |
| 1 |
| 2 |
点评:主要考查了用待定系数法求函数的解析式.先根据条件列出关于字母系数的方程,解方程求解即可得到函数解析式.

练习册系列答案
相关题目
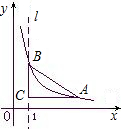 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数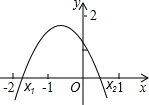 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①b<0;②a+b+c<0;③4a-2b+c<0;④2a-b<0,其中正确的有
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①b<0;②a+b+c<0;③4a-2b+c<0;④2a-b<0,其中正确的有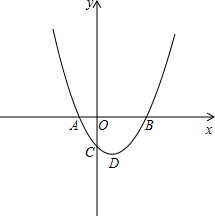 够,求出⊙P的半径;如果不能,请说明理由.
够,求出⊙P的半径;如果不能,请说明理由.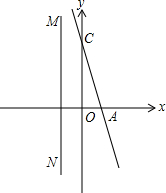 如图,一次函数y=kx+n的图象分别交x轴、y轴与A、C两点.且C点的坐标为(0,3),OC=3OA,直线MN经过点(-1,0)且与x轴垂直,
如图,一次函数y=kx+n的图象分别交x轴、y轴与A、C两点.且C点的坐标为(0,3),OC=3OA,直线MN经过点(-1,0)且与x轴垂直,