题目内容
已知方程组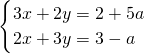
(1)求使它的解满足x+y>0的a的取值范围.
(2)求使不等式x-y>2成立的最小正整数a的值.
解:(1) ,
,
①+②得:5(x+y)=5+4a,
x+y=1+ a,
a,
∵x+y>0,
∴1+ a>0,
a>0,
∴a>- .
.
即使它的解满足x+y>0的a的取值范围是a>- .
.
(2)
①-②得:x-y=-1+6a,
∵x-y>2,
∴-1+6a>2,
∴a> ,
,
∴使不等式x-y>2成立的最小正整数a的值为1.
分析:(1)①+②再除以5即可得出x+y=1+ a,得出不等式,求出不等式的解集即可;
a,得出不等式,求出不等式的解集即可;
(2))①-②即可得出x-y=-1+6a,得出不等式,求出不等式的解集即可
点评:本题考查了解二次一次方程组,解一元一次不等式的应用,关键是能根据题意得出关于a的不等式.
 ,
,①+②得:5(x+y)=5+4a,
x+y=1+
 a,
a,∵x+y>0,
∴1+
 a>0,
a>0,∴a>-
 .
.即使它的解满足x+y>0的a的取值范围是a>-
 .
.(2)

①-②得:x-y=-1+6a,
∵x-y>2,
∴-1+6a>2,
∴a>
 ,
,∴使不等式x-y>2成立的最小正整数a的值为1.
分析:(1)①+②再除以5即可得出x+y=1+
 a,得出不等式,求出不等式的解集即可;
a,得出不等式,求出不等式的解集即可;(2))①-②即可得出x-y=-1+6a,得出不等式,求出不等式的解集即可
点评:本题考查了解二次一次方程组,解一元一次不等式的应用,关键是能根据题意得出关于a的不等式.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目