题目内容
(2002•鄂州)已知抛物线y= mx2-2mx+4m-
mx2-2mx+4m- 与x轴的两个交点的坐标为A(x1,0),B(x2,0)(xl<x2),且x12+x22=34.
与x轴的两个交点的坐标为A(x1,0),B(x2,0)(xl<x2),且x12+x22=34.(1)求m,x1,x2的值;
(2)在抛物线上是否存在点C,使△ABC是一个顶角为120°的等腰三角形?若存在,请求出所有点C的坐标;若不存在,请说明理由.
【答案】分析:(1)本题要根据韦达定理来求解,先表示出x1+x2和x1•x2的值,然后代入x12+x22=34中即可求出m的值,进而可求出x1,x2的值.
(2)如果△ABC是一个顶角为120°的等腰三角形,那么∠CBA=30°,即直线BC的斜率为 ,据此可求出直线BC的解析式,然后联立抛物线的解析式即可求出C点的坐标,然后判断AC是否等于BC或AB是否等于BC即可,再利用C点可能在x轴上方,分别求出即可.
,据此可求出直线BC的解析式,然后联立抛物线的解析式即可求出C点的坐标,然后判断AC是否等于BC或AB是否等于BC即可,再利用C点可能在x轴上方,分别求出即可.
解答:解:(1)令y=0,则有:0= mx2-2mx+4m-
mx2-2mx+4m- ;
;
∴x1+x2=8,x1•x2=
∴x12+x22=(x1+x2)2-2x1x2=64-2× =34
=34
解得m=
∴y= x2-
x2- x+5
x+5
∴ x2-
x2- x+5
x+5 =0,
=0,
解得x1=3,x2=5
(2)假设存在符合条件的C点,那么∠CBA=30°,
设直线BC的解析式为y=kx+b,
则k=tan30°= ,已知B(5,0)
,已知B(5,0)
∴y= x-
x-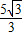
联立抛物线的解析式有:

解得: ,
,
∴存在符合条件的C点,坐标为(4,- ).
).
如图所示:
当AB=BC′时,过点C′作C′E⊥x轴于点E,
∵∠ABC′=120°,则∠C′BE=60°,
∴∠BC′E=30°,
∴BE= BC′=1,
BC′=1,
∴EC′= ,
,
∴C′(6, ).
).
当AC″=AB时,C″(2, ).
).
综上所述:C点坐标为:(4,- ),(6,
),(6, ),(2,
),(2, ).
).
点评:本题主要考查了二次函数与一元二次方程的关系、韦达定理的应用、函数图象交点以及等腰三角形的判定等知识点.
(2)如果△ABC是一个顶角为120°的等腰三角形,那么∠CBA=30°,即直线BC的斜率为
 ,据此可求出直线BC的解析式,然后联立抛物线的解析式即可求出C点的坐标,然后判断AC是否等于BC或AB是否等于BC即可,再利用C点可能在x轴上方,分别求出即可.
,据此可求出直线BC的解析式,然后联立抛物线的解析式即可求出C点的坐标,然后判断AC是否等于BC或AB是否等于BC即可,再利用C点可能在x轴上方,分别求出即可.解答:解:(1)令y=0,则有:0=
 mx2-2mx+4m-
mx2-2mx+4m- ;
;∴x1+x2=8,x1•x2=

∴x12+x22=(x1+x2)2-2x1x2=64-2×
 =34
=34解得m=

∴y=
 x2-
x2- x+5
x+5
∴
 x2-
x2- x+5
x+5 =0,
=0,解得x1=3,x2=5
(2)假设存在符合条件的C点,那么∠CBA=30°,
设直线BC的解析式为y=kx+b,
则k=tan30°=
 ,已知B(5,0)
,已知B(5,0)∴y=
 x-
x-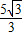
联立抛物线的解析式有:

解得:
 ,
,
∴存在符合条件的C点,坐标为(4,-
 ).
).
如图所示:
当AB=BC′时,过点C′作C′E⊥x轴于点E,
∵∠ABC′=120°,则∠C′BE=60°,
∴∠BC′E=30°,
∴BE=
 BC′=1,
BC′=1,∴EC′=
 ,
,∴C′(6,
 ).
).当AC″=AB时,C″(2,
 ).
).综上所述:C点坐标为:(4,-
 ),(6,
),(6, ),(2,
),(2, ).
).点评:本题主要考查了二次函数与一元二次方程的关系、韦达定理的应用、函数图象交点以及等腰三角形的判定等知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 mx2-2mx+4m-
mx2-2mx+4m- 与x轴的两个交点的坐标为A(x1,0),B(x2,0)(xl<x2),且x12+x22=34.
与x轴的两个交点的坐标为A(x1,0),B(x2,0)(xl<x2),且x12+x22=34. 分别相交于点D和P,连接PB、PC.
分别相交于点D和P,连接PB、PC.