题目内容
画图并计算:已知线段AB=2cm,延长线段AB至点C,使得BC=
AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)哪个点是线段DC的中点?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
| 1 | 2 |
(1)准确地画出图形,并标出相应的字母;
(2)哪个点是线段DC的中点?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
分析:(1)根据题意,做出图形,并且标出相应字母即可;
(2)根据图形,可判断点A为线段DC的中点,根据BC=
AB,AD=AC,计算出线段AB的长所占的比例;
(3)先计算出DC的长度,然后求出BC的长度,用DC-BC可求得BD的长度.
(2)根据图形,可判断点A为线段DC的中点,根据BC=
| 1 |
| 2 |
(3)先计算出DC的长度,然后求出BC的长度,用DC-BC可求得BD的长度.
解答:解:(1)如图:
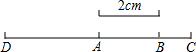 ;
;
(2)线段DC的中点是点A.
∵BC=
AB,
∴AB=
AC,
∵AD=AC,
∴AB=
DC;
(3)∵AB=2cm,
∴DC=3×2=6(cm),BC=
×2=1(cm),
∴BD=DC-BC=6-1=5(cm).
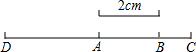 ;
;(2)线段DC的中点是点A.
∵BC=
| 1 |
| 2 |
∴AB=
| 2 |
| 3 |
∵AD=AC,
∴AB=
| 1 |
| 3 |
(3)∵AB=2cm,
∴DC=3×2=6(cm),BC=
| 1 |
| 2 |
∴BD=DC-BC=6-1=5(cm).
点评:本题考查了两点间的距离,解答本题需要我们熟练掌握中点的性质及等量代换思想的运用.

练习册系列答案
相关题目

 AB,再反向延长AC至点D,使得AD=AC.
AB,再反向延长AC至点D,使得AD=AC.