题目内容
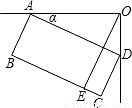
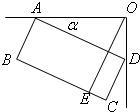7、如图是一台54英寸的大背投彩电放置在墙角的俯视图．设∠DAO=α，彩电后背AD平行于前沿BC，且与BC的距离为55cm，若AO=100cm，则墙角O到前沿BC的距离OE是（ ）分析：设OE、AD相交与F，则EF=55，只要求出OF的长就可以了．在直角三角形AFO中，∵∠DAO=α，AO=100cm∴OF=100sinα，而OE=EF+OF，由此可以求出结果．
解答：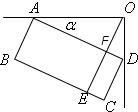
解：设OE、AD相交与F，
则EF=55，
在直角三角形AFO中，
∵∠DAO=α，AO=100cm，
∴OF=100sinα，
∵EF=55，
∴OE=55+100sinαOE=55+100sinα．
故选B．
解：设OE、AD相交与F，则EF=55，
在直角三角形AFO中，
∵∠DAO=α，AO=100cm，
∴OF=100sinα，
∵EF=55，
∴OE=55+100sinαOE=55+100sinα．
故选B．
点评：此题考查了正弦函数的定义与应用，解题的关键是把实际问题转化成数学问题进行解答，在本题中只要构建直角三角形就可以利用正弦求出OE．
练习册系列答案
名校课堂系列答案
相关题目
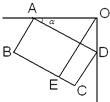16、如图是一台54英寸的大背投彩电放置在墙角的俯视图．设∠DAO=α，彩电后背AD平行于前沿BC，且与BC的距离为60cm，若AO=100cm，则墙角O到前沿BC的距离OE是
19、如图是一台54英寸的大背投彩电放置在墙角的俯视图．设∠DAO=a，彩电后背AD平行于前沿BC，且与BC的距离为60cm，若AO=100cm，则墙角O到前沿BC的距离OE是（ ）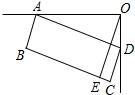
（2012•黄陂区模拟）如图是一台54英寸的大背投彩电放置在墙角的俯视图（其中ABCD是矩形）．设∠ADO=α，彩电后背AD与前沿BC的距离为60cm，若AO=100cm，则墙角O到前沿BC的距离OE是（ ）