��Ŀ����
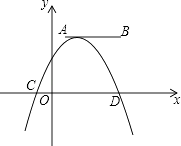
����Ŀ��ij���η羰������һ�ּ���Ʒ���ü���Ʒ�ijɱ�Ϊ12Ԫ/�������ּ���Ʒ�����ۼ۸�Ϊx��Ԫ/������ÿ�����������y������֮��ĺ�����ϵ��ͼ��ʾ�� 
��1����y��x֮��ĺ�����ϵʽ��
��2�����ۼ۸�Ϊ����ʱ��ÿ����Ի�������������������
��3����ʮһ���ڼ䣬�ο�����������ӣ��������۴����ü���Ʒ��Ԥ��ÿ�����������������200%��Ϊ����������ʮһ�����ڸü���Ʒ����ۺ��ۼ�Ϊ���٣�
���𰸡�
��1���⣺��y=kx+b��
���ݺ���ͼ��ɵã� ![]() ��
��
��ã� ![]() ��
��
��y=��5x+200
��2���⣺��ÿ�����wԪ��
��w=��x��12��y=��5x2+260x��2400=��5��x��26��2+980��
�൱x=26ʱ��w����������Ϊ980Ԫ
��3���⣺�衰ʮһ������ÿ������ΪPԪ��
��P=��0.8x��12��y��1+200%��=��12x2+660x��7200=��12��x�� ![]() ��2+1875��
��2+1875��
�൱x= ![]() ʱ��P���
ʱ��P���
��ʱ�ۼ�Ϊ0.8�� ![]() =22��
=22��
�𣺡�ʮһ�����ڸü���Ʒ����ۺ��ۼ�Ϊ22Ԫ
����������1�����ݺ���ͼ��������������꣬���ô���ϵ�������ɵã���2�����ݡ�������=������������������г��������������ö��κ��������ʿɵ���ֵ�������3�����ݣ�2������ȹ�ϵ�г���������ʽ���ɶ��κ������������ɵã�