Question

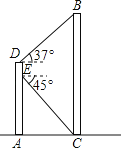
【题目】如图，某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°，此时该同学距地面高度AE为20米，电梯再上升5米到达D点，此时测得大楼BC楼顶B点的仰角为37°，求大楼的高度BC．

（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）．

Answer 1

【答案】大楼BC的高度是40米．

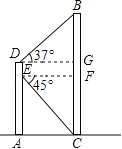
【解析】试题分析：首先过点E、D分别作BC的垂线，交BC于点F、G，得两个直角三角形△EFC和△BDG，由已知大楼BC楼底C点的俯角为45°，得出EF=FC=AE=20，DG=EF=20，再由直角三角形△BDG，可求出BG，GF=DE=5，从而求出大楼的高度BC．

试题解析：解：过点E、D分别作BC的垂线，交BC于点F、G．

在Rt△EFC中，因为FC=AE=20，∠FEC=45°，所以EF=20． 2分

在Rt△DBG中，DG=EF=20，∠BDG=37°,

因为tan∠BDG=≈0．75， 2分

所以BG≈DG×0．75=20×0．75=15，

而GF=DE=5， 2分

所以BC=BG+GF+FC=15+5+20=40．

答：大楼BC的高度是40米． 2分