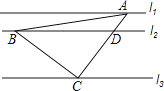
题目内容
【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE= ![]() (AB+AC).
(AB+AC).
【答案】
(1)
证明:∵DA平分∠BAC,
∴∠BAD=∠CAD,
∵AD∥EM,
∴∠BAD=∠AEF,∠CAD=∠AFE,
∴∠AEF=∠AFE,
∴AE=AF
(2)
证明:作CG∥EM,交BA的延长线于G.

∵EF∥CG,
∴∠G=∠AEF,∠ACG=∠AFE,
∵∠AEF=∠AFE,
∴∠G=∠ACG,
∴AG=AC,
∵BM=CM.EM∥CG,
∴BE=EG,
∴BE= ![]() BG=
BG= ![]() (BA+AG)=
(BA+AG)= ![]() (AB+AC).
(AB+AC).
【解析】(1)欲证明AE=AF,只要证明∠AEF=∠AFE即可.(2)作CG∥EM,交BA的延长线于G,先证明AC=AG,再证明BE=EG即可解决问题.本题考查三角形中位线定理、角平分线的性质、等腰三角形的判定和性质等知识,解题的关键是添加辅助线,构造等腰三角形,以及三角形中位线,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】下面是淄博市2016年4月份的天气情况统计表:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 多云 | 阴 | 多云 | 晴 | 多云 | 阴 | 晴 | 晴 | 晴 | 多云 | 多云 | 多云 | 晴 | 晴 | 雨 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 雨 | 多云 | 多云 | 多云 | 多云 | 晴 | 多云 | 多云 | 晴 | 多云 | 多云 | 多云 | 晴 | 晴 | 晴 |
(1)请完成下面的汇总表:
天气 | 晴 | 多云 | 阴 | 雨 |
天数 |
(2)根据汇总表绘制条形图;
(3)在该月中任取一天,计算该天多云的概率.