题目内容
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,以
,以![]() 为圆心,
为圆心, ![]() 长为半径的圆分别交
长为半径的圆分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点.
两点.
(1)求证: ![]() 是
是![]() 的切线;
的切线;
(2)判断由![]() ,
, ![]() ,
, ![]() 及切点所构成的四边形的形状,并说明理由.
及切点所构成的四边形的形状,并说明理由.

【答案】(1)证明见解析;(2)四边形![]() 为菱形,理由见解析.
为菱形,理由见解析.
【解析】试题分析:(1)作OF⊥AC于F,如图,理由三角函数可得到∠A=30°,OA=2OF,再利用BO=![]() AB得到OA=2OB,所以OF=OB,于是根据切线的判定方法可判AC是⊙O的切线;(2)先证明△OFD和△OBE都是等边三角形得到OD=DF,∠BOE=60°,则可计算出∠EOF=60°,从而可判定△OEF为等边三角形,所以EF=OE,则有OD=DF=EF=OE,然后根据菱形的判定方法可判断四边ODFE为菱形.
AB得到OA=2OB,所以OF=OB,于是根据切线的判定方法可判AC是⊙O的切线;(2)先证明△OFD和△OBE都是等边三角形得到OD=DF,∠BOE=60°,则可计算出∠EOF=60°,从而可判定△OEF为等边三角形,所以EF=OE,则有OD=DF=EF=OE,然后根据菱形的判定方法可判断四边ODFE为菱形.
试题解析:
(1)证明:作OF⊥AC于F,如图,
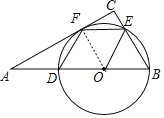
∵∠C=90°,AB=2BC,
∴sinA=![]() =
=![]() ,
,
∴∠A=30°,
∴OA=2OF,
∵BO=![]() AB,
AB,
∴OA=2OB,
∴OF=OB,
∴AC是⊙O的切线;
(2)四边形ODFE为菱形。理由如下:
∵∠A=30°,
∴∠AOF=∠B=60°,
∴△OFD和△OBE都是等边三角形,
∴OD=DF,∠BOE=60°,
∴∠EOF=180°60°60°=60°,
∴△OEF为等边三角形,
∴EF=OE,
∴OD=DF=EF=OE,
∴四边形ODFE为菱形。

练习册系列答案
相关题目




