题目内容
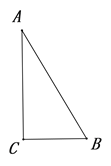
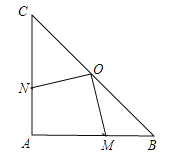
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM .
(1)证明:OM = ON;
(2)四边形AMON面积是否发生变化,若发生变化说明理由;若不变,请你求出四边形AMON的面积.
【答案】(1)见解析 (2)4cm2
【解析】试题分析:
(1) 分析条件可知,要证明OM=ON需要利用全等三角形进行. 易知△ABC是等腰直角三角形,根据“O是BC的中点”这一条件容易联想到利用等腰三角形“三线合一”的性质来构造全等三角形. 连接OA后容易发现△OAN与△OBM全等,进而得到OM=ON.
(2) 借助第(1)小题的辅助线作法可知,AO将四边形AMON分割为△OAN与△OAM. 由第(1)小题的证明可知,△OAN的面积等于△OBM的面积. 利用这一关系,实际上将四边形AMON的面积转化为了△OAB的面积. 因为△OAB的面积不受动点运动的影响,所以四边形AMON的面积不变. 根据等腰三角形的性质容易求得△OAB的面积,即得四边形AMON的面积.
试题解析:
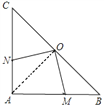
(1) 连接OA. (如图)
∵在Rt△ABC中,AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,即∠ABO=45°,
∵O是BC的中点,且△ABC是等腰直角三角形,
∴AO⊥BC,
∴在Rt△AOB中,∠OAB=90°-∠ABO=90°-45°=45°,
∴∠OAB=∠ABO,
∴OA=OB,
∵O是BC的中点,且△ABC是等腰直角三角形,
又∵∠BAC=90°,
∴![]() ,
,
∴∠OAC=∠ABO=45°,即∠OAN=∠OBM,
∵在△OAN与△OBM中:
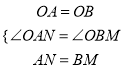 ,
,
∴△OAN≌△OBM (SAS),
∴ON=OM,即OM=ON.
(2) 在动点运动过程中,四边形AMON面积不变.
下面求解四边形AMON的面积.
连接OA.
由第(1)小题的证明可知:△OAN≌△OBM,
∴△OAN的面积等于△OBM的面积,
∵四边形AMON的面积等于△OAN的面积与△OAM的面积之和,
∴四边形AMON的面积等于△OBM的面积与△OAM的面积之和,
∵△OBM的面积与△OAM的面积之和等于△OAB的面积,
∴四边形AMON的面积等于△OAB的面积,
∵O是BC的中点,且△ABC是等腰直角三角形,
∴△OAB的面积等于△ABC的面积的一半,
∵AB=AC=4cm,
∴Rt△ABC的面积为: ![]() (cm2),
(cm2),
∴△OAB的面积为: ![]() (cm2),
(cm2),
∴四边形AMON的面积为:4cm2.