Question

27、挑战自我！
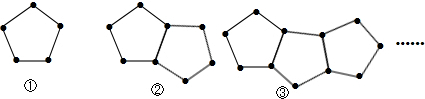
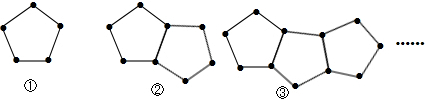
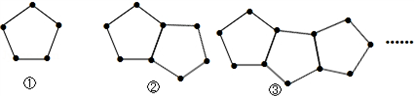
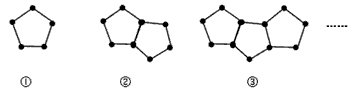
下图是由一些火柴棒搭成的图案：
（1）摆第①个图案用

5

根火柴棒，
摆第②个图案用

9

根火柴棒，
摆第③个图案用

13

根火柴棒．
（2）按照这种方式摆下去，摆第n个图案用多少根火柴棒？
（3）计算一下摆121根火柴棒时，是第几个图案？

Answer 1

分析：解决此题的关键是弄清图案中的规律，根据图片中的三个图案知，每个图案都比上一个图案多一个五边形，但是只增加4根火柴，根据此规律来分析，可得答案．

第①个图案所用的火柴数：1+4=1+4×1=5，
第②个图案所用的火柴数：1+4+4=1+4×2=9，
第③个图案所用的火柴数：1+4+4+4=1+4×3=13，
…
依次类推，第n个图案中，所用的火柴数为：1+4+4+…+4=1+4×n=4n+1；
可根据上面得到的规律来解答此题．

解答：解：（1）由题目得，第①个图案所用的火柴数：1+4=1+4×1=5，
第②个图案所用的火柴数：1+4+4=1+4×2=9，
第③个图案所用的火柴数：1+4+4+4=1+4×3=13，

（2）
按（1）的方法，依次类推，
由规律可知5=4×1+1，9=4×2+1，13=4×3+1，
第n个图案中，所用的火柴数为：1+4+4+…+4=1+4×n=4n+1；
故摆第n个图案用的火柴棒是4n+1；

（3）根据规律可知4n+1=121得，n=30．

点评：主要考查了学生通过特例分析从而归纳总结出一般结论的能力．