题目内容
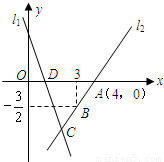
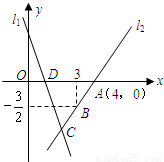
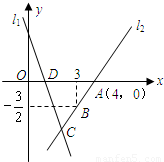
(2008•河北)如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
【答案】分析:(1)已知l1的解析式,令y=0求出x的值即可;
(2)设l2的解析式为y=kx+b,由图联立方程组求出k,b的值;
(3)联立方程组,求出交点C的坐标,继而可求出S△ADC;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,ADC高就是C到AD的距离.
解答:解:(1)由y=-3x+3,令y=0,得-3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;
x=3,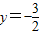 ,
,
∴ ,
,
∴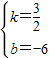 ,
,
∴直线l2的解析表达式为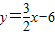 ;
;
(3)由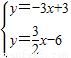 ,
,
解得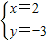 ,
,
∴C(2,-3),
∵AD=3,
∴S△ADC= ×3×|-3|=
×3×|-3|= ;
;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是C到AD的距离,即C纵坐标的绝对值=|-3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x-6,y=3,
∴1.5x-6=3
x=6,
所以P(6,3).
点评:本题考查的是一次函数的性质,三角形面积的计算等有关知识,难度中等.
(2)设l2的解析式为y=kx+b,由图联立方程组求出k,b的值;
(3)联立方程组,求出交点C的坐标,继而可求出S△ADC;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,ADC高就是C到AD的距离.
解答:解:(1)由y=-3x+3,令y=0,得-3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;
x=3,
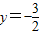 ,
,∴
 ,
,∴
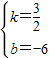 ,
,∴直线l2的解析表达式为
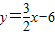 ;
;(3)由
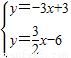 ,
,解得
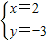 ,
,∴C(2,-3),
∵AD=3,
∴S△ADC=
 ×3×|-3|=
×3×|-3|= ;
;(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是C到AD的距离,即C纵坐标的绝对值=|-3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x-6,y=3,
∴1.5x-6=3
x=6,
所以P(6,3).
点评:本题考查的是一次函数的性质,三角形面积的计算等有关知识,难度中等.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目