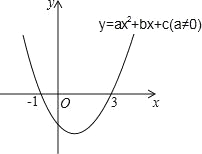
��Ŀ����
����Ŀ���ס�����������ͨA��B��C���صĹ�·����ʻ���׳���A�س���������C����ʻ��ͬʱ�ҳ���C�س���������b����ʻ������B�ز���B��ͣ��1Сʱ��ԭ·ԭ�ٷ��ص�C�أ���������ʻ�Ĺ����У��ס���������B�ص�·��y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ������ͼ��ش��������⣺
��1����ס����������ٶȣ�����ͼ�У� ����������ȷ������
��2�����ҳ���B�ط��ص�C�صĹ����У�y��x֮��ĺ�����ϵʽ��
��3�����ס���������ʻ����B�ص�·�����ʱ���ס���������B�ص�·���Ƕ��٣�
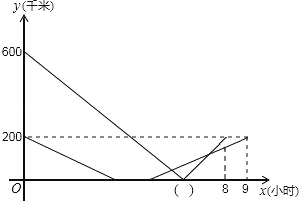
���𰸡���1��6����2��y=50x-250��5��x��9������3��![]() ��100ǧ�ף�
��100ǧ�ף�
��������
�����������1������֪ͼ������ס��ҵ��ٶȣ�
��2������ͼ���ϵĵ�������ҳ���B�ط��ص�C�صĺ�������ʽ��
��3��������׳���A�ص�B�صĺ�������ʽ��y1=k1x+b1���ͼ׳���B�ص�C�صĺ�������ʽ��y2=k2x+b2������֪�������ʽ��ϣ�2������Ľ���ʽ��⣮
�����������1������֪ͼ��ã����ٶ�Ϊ����600+200����8=100km/h���ҵ��ٶ�Ϊ��200+200���£�9-1��=50km/h��
���ٶ�Ϊ��100km/h����B�����600km��
��ʱ��=![]() =6��
=6��
��2�����ҳ���B�ط��ص�C�صĺ�������ʽ��y=kx+b��
���ҵ��ٶ�Ϊ��200+200���£�9-1��=50km/h��
���ҵ�B�ص�ʱ����200��50=4��Сʱ����
4+1=5��
����M��5��0������ͼ��
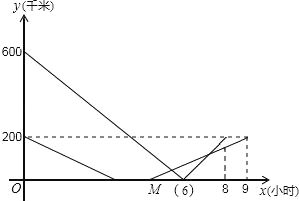
��ͼ��M��5��0������9��200�����㣮
��5k+b=0��9k+b=200
��ã�![]() ��
��
��y=50x-250��
���ҳ���B�ط��ص�C�صĹ����У�y��x֮��ĺ�����ϵʽΪy=50x-250��5��x��9����
��3����׳���A�ص�B�صĺ�������ʽ��y1=k1x+b1��
��ͼ����0��600������6��0�����㣬
��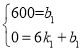 ����ã�
����ã�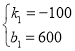 ��
��
��y1=-100x+600��
��׳���B�ص�C�صĺ�������ʽ��y2=k2x+b2��
��ͼ����8��200������6��0�����㣬
��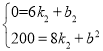 ����ã�
����ã�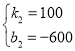 ��
��
��y2=100x-600��
�� ��
��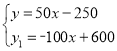 ��
��
��ã�y=![]() ��ǧ�ף���y=100��ǧ�ף���
��ǧ�ף���y=100��ǧ�ף���
�𣺵��ס���������ʻ����B�ص�·�����ʱ���ס���������B�ص�·����![]() ��100ǧ�ף�
��100ǧ�ף�