题目内容
如图,已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE.
(1) 如图所示,观察猜想DE是⊙O的切线吗?并证明你的结论;
(2)  连结OE、AE,当∠CAB为何值时,四边形AOED是平行四边形,并说明理由.
连结OE、AE,当∠CAB为何值时,四边形AOED是平行四边形,并说明理由.
解:(1). 观察猜想DE是⊙O的切线.
证明: 如图,连接OD、DB、OE,.
∵AB是⊙O直径,∴∠CDB=∠ADB=900.
又∵BE=CE,∴ DE=BE.
又∵OD=OB,OE=OE,∴△ODE≌△OBE(SSS).
∴∠ODE=∠OBE=900.
∴DE是⊙O的切线.
(2).当∠CAB=450 时,四边形AOED是平行四边形.
理由是:如图,∵CE=BE,AO=BO,∴OE∥AC.
又∵∠CAB=450 ,∠ABC=900.∴∠C==450 .
∴AB=BC. ∴AD=DC.∴AD=DC. ∴ DE∥AB. ∴四边形AOED是平行四边形.
(其它解法合理,参照给分).
 |

练习册系列答案
相关题目
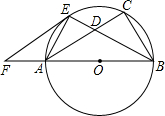 ⊙O于E,过E作EF∥AC交BA的延长线于F.AF=5,EF=10,
⊙O于E,过E作EF∥AC交BA的延长线于F.AF=5,EF=10, ⊙O于E,过E作EF∥AC交BA的延长线于F.AF=5,EF=10,
⊙O于E,过E作EF∥AC交BA的延长线于F.AF=5,EF=10,
