题目内容
求値:
(1)已知m+n=3,mn=1,求m2+n2的値;
(2)已知:am=3,an=5,求 a3m-2n的值.
解:(1)∵m+n=3,mn=1,
∴m2+n2=(m+n)2-2mn=9-2=7;
(2)∵am=3,an=5,
∴a3m-2n=(am)3÷(an)2=27÷25=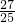 .
.
分析:(1)根据完全平方公式,即可得:m2+n2=(m+n)2-2mn,代入求值即可;
(2)首先将原式变形:a3m-2n=(am)3÷(an)2,然后代入数值求解即可.
点评:此题考查了完全平方公式的变形与幂的性质的逆用.题目难度不大,注意整体思想的应用.
∴m2+n2=(m+n)2-2mn=9-2=7;
(2)∵am=3,an=5,
∴a3m-2n=(am)3÷(an)2=27÷25=
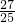 .
.分析:(1)根据完全平方公式,即可得:m2+n2=(m+n)2-2mn,代入求值即可;
(2)首先将原式变形:a3m-2n=(am)3÷(an)2,然后代入数值求解即可.
点评:此题考查了完全平方公式的变形与幂的性质的逆用.题目难度不大,注意整体思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目