题目内容
在纸上剪下一个圆形和一个扇形纸片，使之恰好能够围成一个圆锥模型，若圆的半径为r，扇形的半径为R，扇形的圆心角等于120°（如图），则r与R之间的关系是（ ）
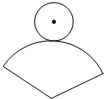
A. R=2r B. R=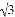
r C. R=3r D. R=4r
练习册系列答案
相关题目
题目内容
在纸上剪下一个圆形和一个扇形纸片，使之恰好能够围成一个圆锥模型，若圆的半径为r，扇形的半径为R，扇形的圆心角等于120°（如图），则r与R之间的关系是（ ）
A. R=2r B. R=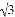r C. R=3r D. R=4r
－cd的值是（ ）
x2﹣2mx﹣4m+1=0有两个相等的实数根，则（m﹣2）2﹣2m（m﹣1）的值为_____．
