题目内容
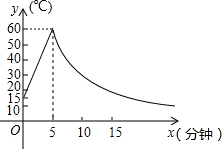 制作一种产品的同时,需将原材料加热,设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,在加热过程中,该材料的温度与时间成一次函数关系;已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例关系(如图).
制作一种产品的同时,需将原材料加热,设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,在加热过程中,该材料的温度与时间成一次函数关系;已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例关系(如图).(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度不低于24℃的这段时间内,需要对该材料进行特殊处理,那么,该材料进行特殊处理所用时间为多少分钟?
分析:(1)确定两个函数后,找到函数图象经过的点的坐标,用待定系数法求得函数的解析式即可;
(2)分别令两个函数的函数值为24,解得两个x的值相减即可得到答案.
(2)分别令两个函数的函数值为24,解得两个x的值相减即可得到答案.
解答:解:(1)设加热过程中一次函数表达式为y=kx+b(k≠0),
该函数图象经过点(0,15),(5,60),
,
解得
∴一次函数的表达式为y=9x+15(0≤x≤5),
设加热停止后反比例函数表达式为y=
(a≠0),该函数图象经过点(5,60),
即a=5×60=300,
所以反比例函数表达式为y=
(x≥5);
(2)当 y=24时,代入y=9x+15有x=1
当 y=24时,代入y=
有x=12.5
12.5-1=11.5(分钟).
答:该材料进行特殊处理所用时间为11.5分钟.
该函数图象经过点(0,15),(5,60),
|
解得
|
∴一次函数的表达式为y=9x+15(0≤x≤5),
设加热停止后反比例函数表达式为y=
| a |
| x |
即a=5×60=300,
所以反比例函数表达式为y=
| 300 |
| x |
(2)当 y=24时,代入y=9x+15有x=1
当 y=24时,代入y=
| 300 |
| x |
12.5-1=11.5(分钟).
答:该材料进行特殊处理所用时间为11.5分钟.
点评:本题考查了反比例函数的应用,解题的关键是从实际问题中整理出函数模型,利用函数的知识解决实际问题.

练习册系列答案
相关题目
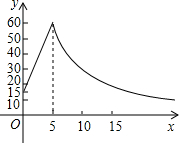 到60℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时问x成反比例函数关系.
到60℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时问x成反比例函数关系.

